Yarılama (İkiye Bölme veya Bisection) Yöntemi

Not

Not

Olmayan sayıyı aramayın. 3. dereceli denklemi örnek alırsak, 3. dereceden denklemde y=0 için çözüm kümesi en fazla üç elemanlıdır.Yani y=0 yapan x değeri, denklemin derecesi kadar olmayabilir. Örneğin 3. dereceden denklemde y=0 yapan x değeri 2 tane olabilir. Yani eğri x eksenini sadece 2 noktadan kesiyor olabilir. Denklemi türevleyip tepe noktalarını bulduğumuzda, tepe noktalarının işaretleri bize bu konuda bilgi verir. Birbirine en yakın iki tepe noktasının işareti aynı ise, o iki tepe noktası arasında y=0 için x değeri yoktur demektir. Bu konuya 4. dereceden bir denklemle örnek verelim.

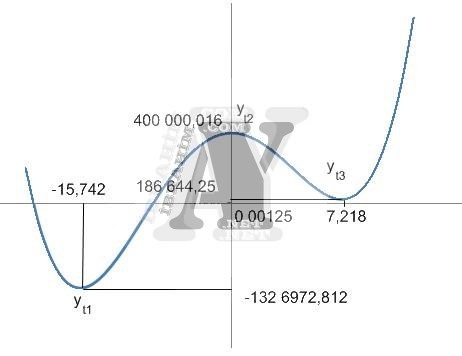
f(x)= 44x⁴ + 500x³ – 10000x² + 25x + 400000 denklemine ait eğrinin tepe noktalarına bakalım.

Üstteki 4. dereceden bir denklem olduğu için (4-1=3) tepe noktası vardır.

f(x)’=176x³ + 1500x²-20000x+ 25

f(x)’=0 için çözüm kümesini bulduğumuzda x₁= 7,218 x₂= -15,742 x₃= 0,00125

Denklemin tepe noktaları

f(7,218)= 44x⁴ + 500x³ – 10000x² + 25x + 400000=186 644,25

f(-15,742)= 44x⁴ + 500x³ – 10000x² + 25x + 400000=-132 6972,812

f(0,00125)= 44x⁴ + 500x³ – 10000x² + 25x + 400000=400 000,016

Tepe noktalarını küçükten büyüğe sıraya koyalım

-132 6972,812__________ 186 644,25__________ 400 000,016

y=0 için x, ilk iki tepe noktası arasında mevcut (y_t1*y_t2<0). Ancak son iki tepe noktası aynı işaretli ve y=0 için x değeri yok (y_t2*y_t3).

Dolayısıyla 4. dereceden denklemimizin çözüm kümesinde 2 değer vardır.