Yarılama (İkiye Bölme veya Bisection) Yöntemi

Yüksek Dereceli Denklemler

Yüksek Dereceli Denklemler

Bu yöntem ile 3’ten yüksek dereceli denklemleri çözmeye çalışmanız yorgunluk, halsizlik, matematikten nefret gibi yan etkilere sebebiyet verebilir. Demek istediğim bu yöntemle yüksek dereceli denklemleri çözmeye çalışmak zaman kaybıdır.Yarıya bölme yöntemi ln, e, cos,.. gibi ifadeler içeren, x’in tek başına bırakılmasının zor olduğu durumlar için ilaçtır. 3. Dereceden bir denklemi çözmek için tepe noktalarını bulun, gerisi gelir.

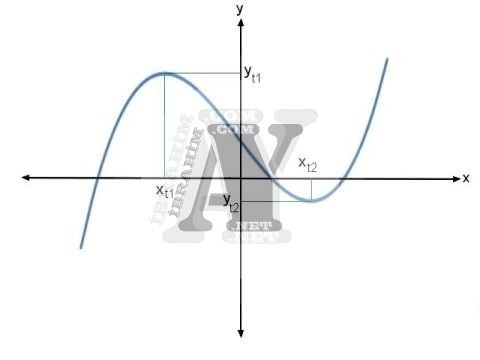
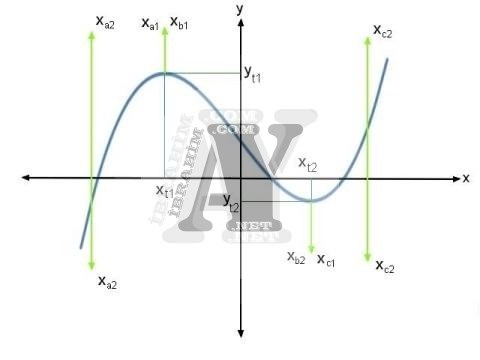
3. dereceden denklemin 2 tepe noktası vardır. Denklemin türevi alındığından 2. dereceden denklem elde edilecektir. Denklemin türevinin çözüm kümesi tepe noktalarını vereceğinden bahsetmiştik. 2. dereceden denklemde 2 bilinmeyen olduğu için, 3. derecede denklemin de 2 tepe noktası var demektir.

Denklemin türevinin çözüm kümesi bulunduktan sonra, sadece 2 değeri tahmin etmek bize kalır. Kullanacağımız başlangıç değerleri için tepe noktalarını kullanacağız. Tepe noktalaları dışındaki 2 noktayı (x_a2ve x_c2)biz tahmin edeceğiz. Aşağıdaki resimde başlangıç değerlerimizin yerleri bellidir. Gerisini siz halledebilirsiniz.