Yarılama (İkiye Bölme veya Bisection) Yöntemi

Grafik Çizerek Çözüme Başlamak

Grafik Çizerek Çözüme Başlamak

Şimdi de 2. dereceden bir denklemin çözüm örneğine bakalım.

y=ax²+bx+c

f(x) = 8x²+ 4x -60 denkleminde

y=0 için x=?

Denklem y=0 için x eksenini kesmektedir.Aksi takdirde çözüm kümesi için x yoktur, tanımsızdır. Karşılaştığınız sorularda eğrinin x eksenini kesip kesmediğini kontrol ediniz.

Örneğin aşağıdaki eğriye sahip 2. derecede denklemde y=0 için x değeri yoktur.

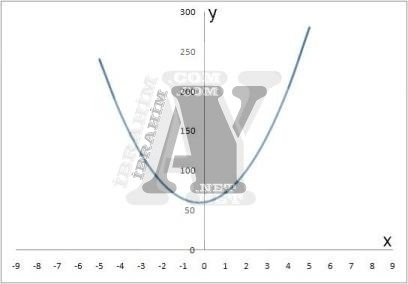
Bu vb. yüksek dereceli denklemleri çözebilmek için ya taslak olarak bir grafik çizmeliyiz ya da tepe noktalarını belirleyerek tahminde bulunmalıyız.

Tepe noktalarının tespiti ile tahmini değerleri bulmayı bir sonraki örnekte anlatacağım.Bu işlem için en azında basitçe türev almayı bilmeliyiz.

Bu aşama da grafik çizim ile çözelim. Grafiğin çok hassas olması önemli değil. Maksat y=0 noktalarını hangi aralıklarda olduğunu görmektir. y=0 noktaları diyoruz, çünkü derecesi 1’den büyük olan denklemlerin çözüm kümesinde 1’den fazla eleman vardır ve x’i birden fazla noktadan kesebilirler. 4. dereceden bir denklemin y=0 çözüm kümesinde en fazla 4 eleman olabilir. (y=0 yapan en fazla 4 farklı x değeri vardır.) ve x’i en fazla 4 noktadan keserler. En fazla diyorum çünkü 4. dereceden bir denklemde eğri x noktasını daha az noktadan kesebilir ve derecesi kadar x değeri olmayabilir.

Bir önceki sorumuz 1. dereceden bir denklemdi. Dolayısıyla çözüm kümesinde 1 eleman vardı ve x’i en fazla bir noktadan kesiyordu.

Bu sorumuz 2. dereceden bir denklem olduğu için x’i iki noktadan keser ve y=0 için iki farklı x değeri vardır. Bu anlattıklarım y=0’ı sağlamayan çözüm kümesi boş denklemler için geçerli değildir. Zira her denklem y=0’ı sağlayacak diye bir şart yok.

2. dereceden denklemleri yarıya bölme yönteminden daha basit bir yöntemle çözebiliriz. Konu anlatımı için yarıya bölme yöntemini kullanacağız. Denklemi 2. dereceden denklemler için kullandığımız basit formülle çözüp kıyaslama yaparız.

Önce kaba taslak bir grafik çizelim.

Ben -44 aralığında bir grafik çiziyorum.

x için 0, 2, 4, -2, -4 noktalarını belirleyeceğim.

f(x) = 8x²+ 4x -60 denkleminde

f(-4) = 52……….f(-2) = -36……….f(0) = -60……….f(2) = -20……….f(4) = 84

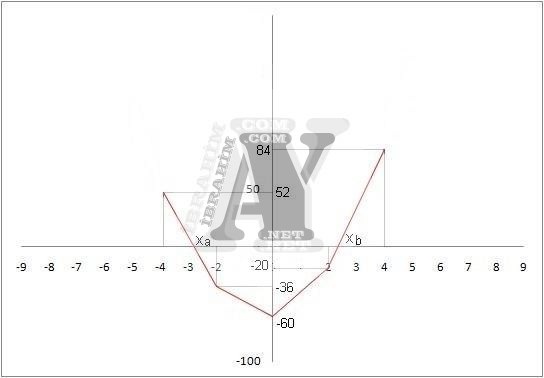
y=0 için iki tane x değeri vardır ve her ikisi içinde ayrı ayrı çözüm yapılmalıdır.

y=0 için x_a =? x_b =?

Çizdiğimiz taslak grafiğe bakarak

x_a‘nın çözümü için x_a1 =-4 x_a2 =-2 değerlerini,

x_b‘nin çözümü için x_b1 =2 x_b2 =4 değerlerini, alabiliriz.

Başlangıç değerlerinin yakın almamak işlemlerimizi çok uzatmaz. Bunu göstermek için -4 ve -2 ile başlamak yerine -7 ve 0 gibi uzak değerlerle başlayacağım. Normalde -4 ve -2 bize uygundur.

x_a‘nın çözümü için x_a1 =-7 x_a2 =0 değerlerini,

x_b‘nin çözümü için x_b1 =0 x_b2 =7 değerlerini, alacağım. Bu değerler yapacağım işlemde adım sayısını korkulacak kadar arttırmaz..

x_a‘nın çözümü için hesabımız

f(x_a1) = 8x_a1²+ 4x_a1 -60 = 8(-7)²+ 4(-7) -60 =304

f(x_a2) = 8x_a2²+ 4x_a2 -60 = 8(0²⁾+ 4(0) -60 =-60

x₃= (x₁+x₂)/2=(-7+0)/2=-7/2=-3,5

f(x_a3) = 8x_a3²+ 4x_a3 -60 = 8(-3,5²⁾+ 4(-3,5) -60 =24

Adım	xa1	xa2	xa3	f(xa1)	f(xa2)	f(xa3)
1	-7,000000	0,000000	-3,500000	304,0000	-60,0000	24,0000

y=0 değerimiz f(x_a2)ile f(x_a3)arasında kaldı. Yeni değerlerimiz için bu iki denkleme ait x_a2 ve x_a3 değerleri ile devam edeceğiz.Dolayısıyla x_a2‘yi değiştirmiyoruz, x_a1 yerine x_a3‘ü yazacağız.

Adım	xa1	xa2	xa3	f(xa1)	f(xa2)	f(xa3)
1	-7,000000	0,000000	-3,500000	304,0000	-60,0000	24,0000
2	-3,500000	0,000000

x₃= (x₁+x₂)/2=(-3,5+0)/2=-3,5/2=-1,75

Adım	xa1	xa2	xa3	f(xa1)	f(xa2)	f(xa3)
1	-7,000000	0,000000	-3,500000	304,0000	-60,0000	24,0000
2	-3,500000	0,000000	-1,750000

f(x_a1) =8x_a1²+ 4x_a1 -60 = 8(-3,5²⁾+ 4(-3,5) -60 =24

f(x_a2) =8x_a2²+ 4x_a2 -60 = 8(0²⁾+ 4(0) -60 =-60

f(x_a3) = 8x_a3²+ 4x_a3 -60 = 8(-1,75²⁾+ 4(-1,75) -60 =-42,5

Adım	xa1	xa2	xa3	f(xa1)	f(xa2)	f(xa3)
1	-7,000000	0,000000	-3,500000	304,0000	-60,0000	24,0000
2	-3,500000	0,000000	-1,750000	24,0000	-60,0000	-42,5000

İşlemlerimizi aynı döngü ile sürdürüyoruz.

Adım	xa1	xa2	xa3	f(xa1)	f(xa2)	f(xa3)
1	-7,000000	0,000000	-3,500000	304,0000	-60,0000	24,0000
2	-3,500000	0,000000	-1,750000	24,0000	-60,0000	-42,5000
3	-3,500000	-1,750000	-2,625000	24,0000	-42,5000	-15,3750
4	-3,500000	-2,625000	-3,062500	24,0000	-15,3750	2,7813
5	-3,062500	-2,625000	-2,843750	2,7813	-15,3750	-6,6797
6	-3,062500	-2,843750	-2,953125	2,7813	-6,6797	-2,0449
7	-3,062500	-2,953125	-3,007813	2,7813	-2,0449	0,3442
8	-3,007813	-2,953125	-2,980469	0,3442	-2,0449	-0,8563
9	-3,007813	-2,980469	-2,994141	0,3442	-0,8563	-0,2575
10	-3,007813	-2,994141	-3,000977	0,3442	-0,2575	0,0430
11	-3,000977	-2,994141	-2,997559	0,0430	-0,2575	-0,1074
12	-3,000977	-2,997559	-2,999268	0,0430	-0,1074	-0,0322
13	-3,000977	-2,999268	-3,000122	0,0430	-0,0322	0,0054
14	-3,000122	-2,999268	-2,999695	0,0054	-0,0322	-0,0134
15	-3,000122	-2,999695	-2,999908	0,0054	-0,0134	-0,0040
16	-3,000122	-2,999908	-3,000015	0,0054	-0,0040	0,0007

16. adımda 1/1000 hassasiyeti yeterli görüp çözümü bitiriyorum.

y=0 için x_a= -3,000015

x_b‘nin çözümü için hesabımız başlangıç değerlerimiz 0-7 aralığında:

Adım	xb1	xb2	xb3	f(xb1)	f(xb2)	f(xb3)
1	0,000000	7,000000	3,500000	-60,0000	360,0000	52,0000
2	0,000000	3,500000	1,750000	-60,0000	52,0000	-28,5000
3	1,750000	3,500000	2,625000	-28,5000	52,0000	5,6250
4	1,750000	2,625000	2,187500	-28,5000	5,6250	-12,9688
5	2,187500	2,625000	2,406250	-12,9688	5,6250	-4,0547
6	2,406250	2,625000	2,515625	-4,0547	5,6250	0,6895
7	2,406250	2,515625	2,460938	-4,0547	0,6895	-1,7065
8	2,460938	2,515625	2,488281	-1,7065	0,6895	-0,5145
9	2,488281	2,515625	2,501953	-0,5145	0,6895	0,0860
10	2,488281	2,501953	2,495117	-0,5145	0,0860	-0,2147
11	2,495117	2,501953	2,498535	-0,2147	0,0860	-0,0644
12	2,498535	2,501953	2,500244	-0,0644	0,0860	0,0107
13	2,498535	2,500244	2,499390	-0,0644	0,0107	-0,0269
14	2,499390	2,500244	2,499817	-0,0269	0,0107	-0,0081
15	2,499817	2,500244	2,500031	-0,0081	0,0107	0,0013
16	2,499817	2,500031	2,499924	-0,0081	0,0013	-0,0034
17	2,499924	2,500031	2,499977	-0,0034	0,0013	-0,0010
18	2,499977	2,500031	2,500004	-0,0010	0,0013	0,0002

Buradaki hesapta da 18. adımda 1/1000 hassasiyet ile çözümü bitiriyorum. y=0 için x_b= 2,500004

y=0 için x değerlerim -3,000015 ve 2,500004

Aslında çözümü ilerlettikçe x’lerin -3 ve 2,5’a doğru gittiği görülür. Adımları ilerletirseniz net sonuca gidersiniz.

2. dereceden denklemler için kullandığımız formül ile hesabımızı karşılaştıralım.

-3–3,000015

2,52,500004