Yarılama (İkiye Bölme veya Bisection) Yöntemi
Giriş
İçindekiler
Yarılama (İkiye Bölme veya Bisection) Yöntemi “1 bilinmeyenli” denklemlerde y=0 yapan x değerini bulmak için kullanılan çözüm yöntemlerinden biridir.
Örneğin aşağıdaki gibi bir eğriye sahip denklemimiz olduğunu varsayalım. Resmin çok karmaşık olmaması için 1. dereceden bir eğri örneği ile konuyu anlatmaya başlayacağım. Maksadım, yöntemin mantığını izah etmek.
Çözüme başlarken tahmini olarak 2 tane x değeri belirlenir.
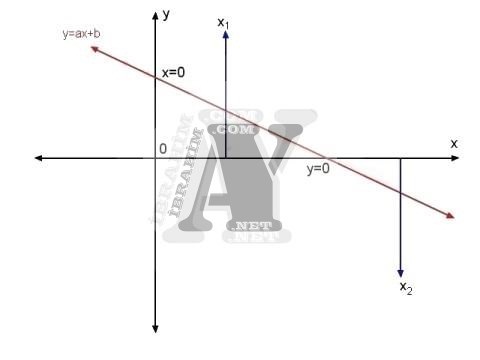
Dikkat edilecek husus, bu başlangıç değerlerimiz olacak olan x’ler y=0 noktasının sağında ve solunda olmalıdır. Diğer bir ifade ile x1 ve x2‘lerimizden biri y<0 diğeri y>0 yapan değerler olmalıdır.
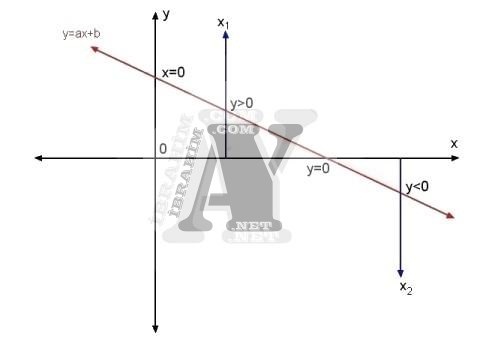
Çözüme x1 ve x2 ile başlamıştık. y=0 için x değeri x1 ile x2 arasındadır.
x1 ile x2‘nin orta noktasında üçüncü bir x değeri olan x3‘ü belirliyoruz.
x3= (x1+x2)/2
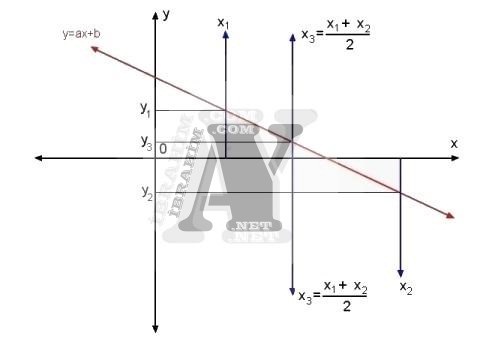
Şu durumda y=0 yapan x değerimiz x2 ile x3 arasında kaldı.
Şimdi y=0 yapan x değerine daha da yaklaşmak için x2 ile x3 değerlerini başlangıç değerleri olarak kabul edeceğiz ve işlemi sürdüreceğiz. x2 ile x3 değerlerini seçmemizin sebebi y=0 yapan x değerinin bu iki değer arasında kalmış olmasıdır.
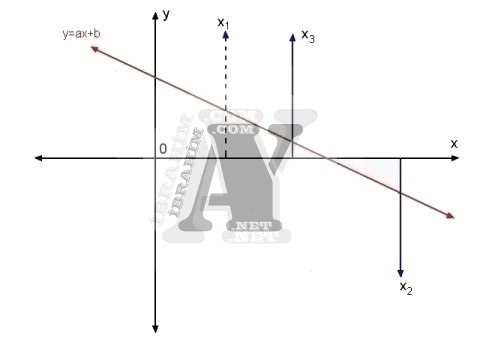
Şimdi x2 ile x3‘ün orta noktasından yeni bir x değeri olan x4‘ü belirliyoruz.
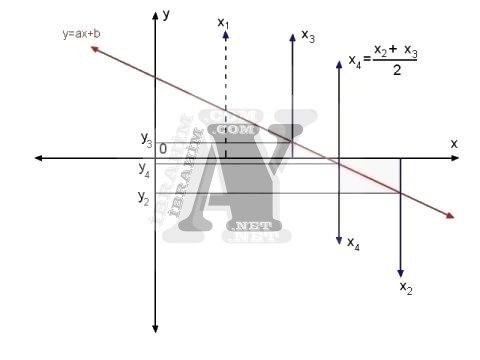
x4‘ten elde ettiğimiz y değeri 0’a yaklaşıyor. Şu durumda y=0 yapan x değeri x3 ile x4 arasında kaldı. Öyleyse başlangıç değerleri olarak x3 ve x4 ile devam edeceğiz.
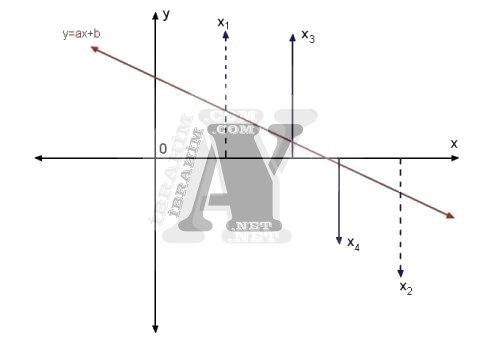
Tekrar yeni bir x değeri olan x5‘i belirleyeceğiz.
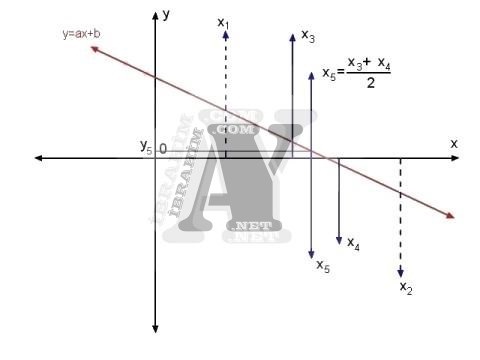
y=0 yapan x değeri bu sefer x4 ile x5 arasında kaldı. İşlem y=0 yapan xn değerine kadar sürdürülür.
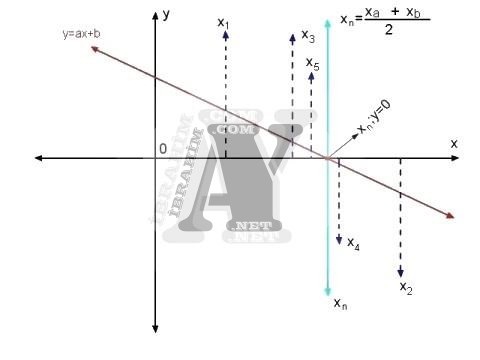
Görüldüğü gibi her iki x başlangıç değerlerimizin orta noktasındaki x değerimiz, gittikçe y=0 yapan x değerine yaklaşmaktadır. Şimdi bu işlemleri sayısal olarak yapalım.
Sayısal çalışmada bir tablo oluşturacağız:
|
Adım
|
x1
|
x2
|
(x1+x2) /2 |
f(x1)
|
f(x2)
|
f(x3)
|
y=f(x)
f(x3)=0 yapan x3 değeri y=0 yapan x değerimizdir. 1. adımda öncelikle başlangıç değerlerimiz olan x1 ve x2 belirlenir. Denklemde x1 ve x2‘lerimizden biri y<0 diğeri y>0 yapan değerler olmalıdır.
|
Adım
|
x1
|
x2
|
x3
|
f(x1)
|
f(x2)
|
f(x3)
|
|
1
|
x1
|
x2
|
(x1+x2) /2
|
f(x1)<0
|
f(x2)>0
|
f(x3)
|
veya
|
Adım
|
x1
|
x2
|
x3
|
f(x1)
|
f(x2)
|
f(x3)
|
|
1
|
x1
|
x2
|
(x1+x2) /2
|
f(x1)>0
|
f(x2)<0
|
f(x3)
|
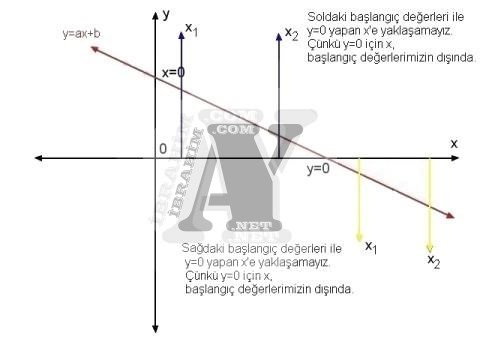
1’den yüksek dereceli denklemlerde y<0 ve y yapan x’lerimizi seçerken daha hassas olacağız. Çünkü 1’den yüksek dereceli denklemlerin 1’den fazla çözüm kümesi vardır. x1 ile x2‘nin ortalamasına da (orta noktasına da) x3 diyeceğiz.(x1 ile x2 toplamının yarısı)
Denklemde (fonksiyonda) x yerine x1 değeri yazarak neticeyi tabloda f(x1) sütununa x yerine x2 yazarak f(x2)’yi x yerine x3 yazarakta f(x3)’ü yerlerine yazacağız. 1. adımımız bitmiş olacak.
|
Adım
|
x1
|
x2
|
x3
|
f(x1)
|
f(x2)
|
f(x3)
|
|
1
|
x1
|
x2
|
(x1+x2) /2
|
y=f(x1)
|
y=f(x2)
|
y=f(x3)
|
2. adımda karşılaştırma yapacağız. y=0 yapan x değerimiz, x1 ile x3 arasında mı? x2 ile x3 arasında mı?
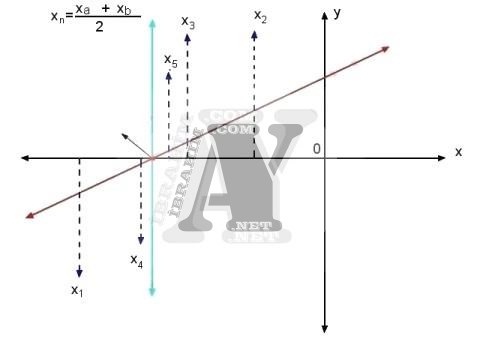
Örneğin aşağıdaki grafiğe baktığımızda y=0 x2 ile x3 arasındadır.

x3 değerimiz x1 ile x2 arasında bir değer olduğu için yukarıdaki önermelerden birisi muhakkak gerçekleşecektir. Yani y=0 yapan x değerimiz, x1 ile x3 arasında ya da x2 ile x3 arasında kalacaktır. Eğer y=0 yapan x değer başlangıçta alınan x1 ile x2 değerleri arasında değilse, yani x değerlerinden biri y<0, diğeri y>0 koşulunu sağlamıyorsa zaten işlemin ilk adımı yanlış başlanmıştır.
2. adımda kullanacağımız başlangıç değerimizden biri x3 olacaktır. Ancak x3‘ü x1‘in yerine mi yoksa x2‘nin yerine mi kullanacağız? Bunun için f(x)=0’ın x1 ile x3 arasında mı yoksa x2 ile x3 arasında mı olduğuna bakılarak karar verilir. Eğer f(x)=0 x1 ile x3 arasında kalmışsa, 2. adımda x1 değiştirilmez, x2 yerine x3 değerini yazarız.
Eğer f(x)=0 x2 ile x3 arasında kalmışsa, 2. adımda x2 değişmez x1 yerine x3 değerini yazarız. Diyelim ki x1 ile x3 arasında kaldı. 2. adım değerleri şöyle olur:
|
Adım
|
x1
|
x2
|
x3
|
f(x1)
|
f(x2)
|
f(x3)
|
|
1
|
x1
|
x2
|
(x1+x2) /2
|
f(x1)<0
|
f(x2)>0
|
f(x3)>0
|
|
2
|
x1
|
x3
|
(x1+x3) /2
|
f(x1)
|
f(x3)
|
f(x4)
|
Bu belirlemeyi yapmanın birden fazla yolu vardır. Çözümün mantığını anladıktan sonra farklı değerlendirme yöntemleri belirleyebilirsiniz. Ben sadece işin mantığını açıklayan belirlemeyi izah ettim.
Ben işlemleri eksel vb yazılımlarda kullanmak için x’lerin tespitlerinde aşağıdaki önermeyi kullanıyorum:
x1 için f(x1)*f(x3)<0 ise x1; x3
x2 için f(x2)*f(x3)<0 ise x2;x3
Yukarıdaki iki önermeden sadece biri gerçekleşecek ve x1 veya x2‘den sadece biri değişecektir. Çünkü başlangıç değerlerimiz y=0 yapan x değerlerinin sağında ve solundadır. x1 ve x2 değerlerinin neticeleri olan f(x)’lerin biri pozitif, diğeri negatif çıkacaktır, yani x1 ile x2‘nin işareti farklı çıkacaktır. Eğer işaretleri farklı çıkmaz ise, zaten başlangıç değerleri olan x’lerden birinin y<0 ve diğerinin y>0 olması gerektiği koşullarına uyulmamış demektir.
f(x)’lerin işaretleri aynı ise, y=0 ( f(x)=0 )’ın o aralıkta olmadığı bellidir. y=0 pozitif ve negatif değerler arasındadır.
İkinci adımdaki başlangıç değerlerimizi de böylece belirledikten sonra, 1. adımda yaptığımız gibi f(x)’ler hesaplanır ve tekrar değerlendirme yapılarak 3. adıma geçilir.
Örneğin
|
Adım
|
x1
|
x2
|
x3
|
f(x1)
|
f(x2)
|
f(x3)
|
|
1
|
x1
|
x2
|
(x1+x2) /2
|
f(x1)<0
|
f(x2)>0
|
f(x3)>0
|
|
2
|
x1
|
x3
|
x4 =
(x1+x3) /2
|
f(x1)<0
|
f(x3)>0
|
f(x4)<0
|
|
3
|
x4
|
x3
|
x5 = (x3+x4) /2
|
f(x4)<0
|
f(x3)>0
|
f(x5)>0
|
|
4
|
x4
|
x5
|
x6 = (x4+x5) /2
|
f(x4)<0
|
f(x5)>0
|
f(x6)>0
|
|
n
|
xa
|
xb
|
xn = (xa+xb) /2
|
f(xa)
|
f(xb)
|
f(xn)=0
|
Bu işlemler f(x3)=0 olana kadar tekrarlanır. f(x3)=0 yapan x3 değerimiz y=0 yapan x değerimizdir.
Her hesapta f(x3)=0 ve x3 tam sayı çıkmayabilir. İşlemler sonsuz adıma kadar uzayabilir. Biz işlemlerimizin hassasiyetine göre belli bir noktada ilerlemeyi bırakabiliriz.
Örneğin 1/1000 (binde 1) hassayeti yeterli görüp bırakabiliriz. Mesela adım 5’te f(x3)=0,00023 gibi bir değer bulduğumuzda işlemi bırakabiliriz. 0<<0,00023 olarak kabul edilebilir.f(x)=0 için 5. adımdaki x değerini kullanabiliriz.
f(x)=0’a en yakın x değerini istediğiniz hassasiyette bulabilirsiniz. Adımları ilerlettikçe hassasiyet artar.