SPSS 8.0 Kullanma Kılavuzu
Korelasyon (Correlation)
İçindekiler
Korelasyon (Correlation)
Elinizdeki iki değişken arasında bir ilişki olup olmadığını görmek için (korelasyon) Statistics/Correlate/Bivariate seçenegini kullanın.
Dikkat etmeniz gereken nokta, değişkenlerinizin her ikisinin sayısal (numaric) olmasıdır. Korelâsyon, değişkenlerinizin birindeki bir değişiklik, aynı oranda diğerinde de beklenebilir mi sorusuna verilen cevaptır. Burada kilo ve boy değişkenlerine bakılıyor. Kilosu yüksek olan birinin boyu da uzun olabilir mi diye korelâsyona bakıyoruz. Korelâsyon katsayısı (r) 0 ile 1 arasında bir değer alır. 0 hiç ilişki olmadığını, 1 ise tam bir ilişki olabileceğini bildirir. Katsayı + ya da olabilir. Örneğin +0.78 olursa iki değişken arasında pozitif bir ilişki var demektir. Biri artınca diğeri de artacaktır diye beklenir. 0.89 olursa, biri artınca diğeri azalacaktır ve negatif ilişki vardır denir. Ancak korelasyon bir neden sonuç ilişkisi değildir.
Not: Korelâsyon yerine “ilgileşim” in kullanılmasını tercih etmekle beraber, kaynağa sadık kalmak için değiştirmedim. (ibrahimay)
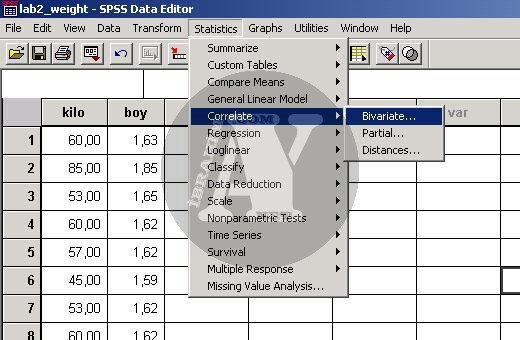
Correlation/ Bivariate
Bu pencerede değişkenlerinizi seçmeniz gerekiyor. Pencerenin sol tarafında var olan değişkenleri göreceksiniz. Bunlardan korelâsyonuna bakmak istediklerinizi seçip sol tarafa geçirin. En az iki ya da daha fazla olabilir. Eğer 4 değişken seçerseniz, bu değişkenlerin kendi aralarında 2’li korelâsyonlarını elde edersiniz.
Otomatik olarak Pearson katsayısı seçilidir. Bu değer normal ölçümler için geçerlidir. Spearman katsayısı ise, değişkenleriniz sıralanmış değerler ise kullanılır. Mesela birinci değişken 10 kişinin sınıf içindeki sıralamalarını (1’inci, 2’nci,.)? ikinci değişken ise bu kişilerin yine yıl sonundaki sıralamalarını veriyorsa, bu sıralamalar arasındaki korelasyonu bulmak için Spearman katsayısını seçin.
Eğer hipotez test etmiyorsanız, Test of significance’i Twotailed bırakın. Ediyorsanız siz karar verin. Options seçeneği ile ek özelliklere ulaşabilirsiniz.
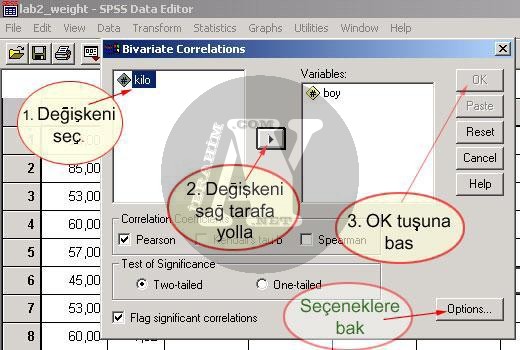
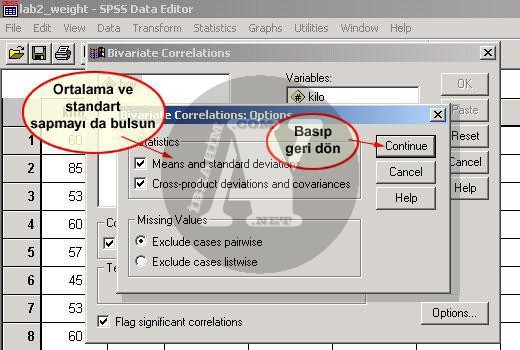
Correlation/ Bivariate/Options Seçeneği
Bu bölümde korelasyon katsayısının yanı sıra ortalama ve standart sapmayı da (means and standard deviations) hesaplatabilmeniz için seçenekler vardır. Bu seçenekleri seçerseniz, çıktı ekranınızda ikinci bir tablo olarak ortalama ve standart sapma da yer alır
Korelâsyon Çıktı Ekranı
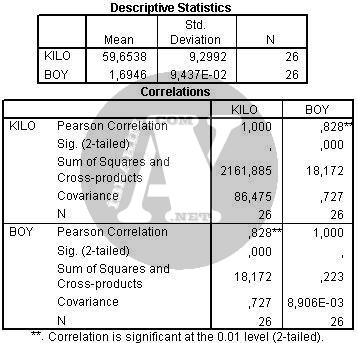
Bu tablolardan ilki, Descriptives, Options bölümünde seçtiğiniz ortalama ve standart sapmayı veren tablodur.
İkinci ve asıl tablo ise değişkenlerin ilişkilerini vermektedir. Pearson Correlation satırında yer alan sayılar korelasyon katsayısını vermektedir. Dikkat ettiyseniz, tablonun KILO adında hem bir satırı ve hem de bir sütunu bulunmaktadır. Bu iki sütunun kesişimde olan hücreleri dikkate almayınız. Önemli olan farklı iki değişkenin kesiştiği hücrelerdir. KILO ve BOY değişkenlerinin kesiştiği hücrede katsayı 0,828 olarak verilmiştir. Bu değer pozitif ve yüksek bir korelâsyonun var olduğunu belirtir. Aynı zamanda Sig.(2tailed) satırlarında da 0,000 olarak verilen değerler, bulduğumuz korelasyon katsayısının 0,01 manidarlık düzeyinde geçerli bir korelasyon katsayısı olduğunu belirtir. Zaten geçerli olan katsayıların yanında, SPSS tarafından basılan iki yıldız (**) işareti vardır.
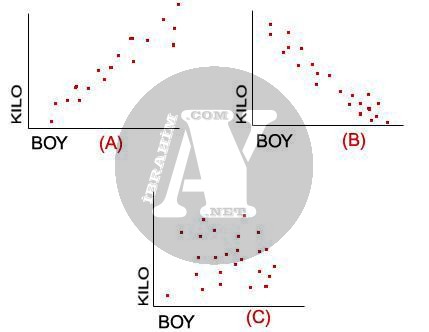
Nokta Dağılımı
Bir önceki bölümde bahsettiğimiz korelasyon katsayısı, aynı zamanda iki değişken arasındaki noktasal dağılım grafiğinin de şeklini belirler. Eğer iki değişken arasında tam bir ilişki varsa, (r) korelasyon katsayısını +1’e yakın bir değerde bulursunuz. Bu durumda bu iki değişkenin ilişkisi sağdaki ilk grafik (A) ile anlatılabilir. KILO attıkça, BOY da artıyor. Eğer r, 1′ e yakın bir değer alırsa, bu ikinci grafik (B) ile örtüşür. Her iki durumda da ilişki kuvvetlidir. Ancak üçüncü grafik (C) gibi bir dağılım elde ederseniz, (r) katsayı 0’a yakın demektir ve bir ilişkiden söz edilemez.
Bu grafikler ile iki değişken arasındaki katsayının neyi anlattığı daha rahat anlaşılır. SPSS’de bu grafiği Graphs/Scatter… seçeneği ile elde edebilirsiniz.
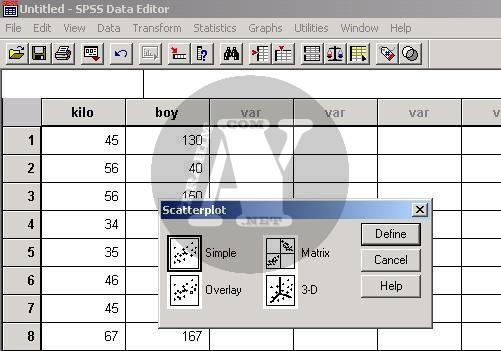
Graph/ Scatter
Bu seçeneği seçtikten sonra karşımıza sağ tarafta görünen küçük Scatterplot penceresi gelecektir. Bu pencereden Simple seçeneğini seçin ve Define’ı tıklayarak devam edin.
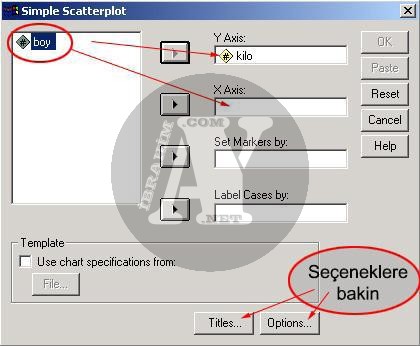
Graph/ Scatter/Simple Scatterplot
Karşınıza gelecek bu menüde, değişkenlerinizi seçeceksiniz. Sol taraftan iki değişkeninizi Y Axis ve X Axis diye adlandırılan kutulara yerleştirin. Bunu ortadaki küçük butonlarla yapabilirsiniz. Hangi değişkeni Y Axis ya da X Axis kutusuna koyduğunuz fark etmez. Y Axis kutusuna KILO değişkenini koyarsanız, grafikteki Y ekseninde KILO değişkeni temsil edilmiş olur. Title ve Options seçeneklerini kullanarak bazı ayarlamalar yapabilirsiniz. Bunları yapmasanız da olur. OK butonuna basınca grafiğiniz Output penceresinde oluşacaktır.
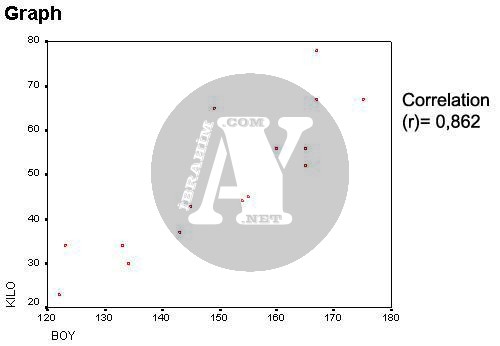
Graph/ Scatter/Simple Scatterplot/Grafik
Çıktı olarak elde ettiğimiz grafik aşağıdaki gibi olacaktır. Bu grafikte kırmızı noktaların X ve Y ekseni üzerinde dek geldiği yer, o kişinin kilosunu ya da boyunu göstermektedir. Gördüğünüz gibi noktaların yerleşimi kilo arttıkça boy da artacak şekildedir. Doğrusal bir çizgi halinde olmasa da, böyle bir doğrusal çizgiye yaklaşmış olmaları, aralarında pozitif ve yüksek bir ilişki olacağını gösteriyor. Hakikaten de, korelasyon katsayısını (r) hesapladığımız zaman, 0,862 olarak hesaplıyoruz. Bu iki sonuç, kilodaki bir artışın, boyda da bekleneceğini ve bu iki değişkenin birbiriyle ilişkili olduğunu belirtiyor.