Minitab İle Regresyon Analizi

Regression

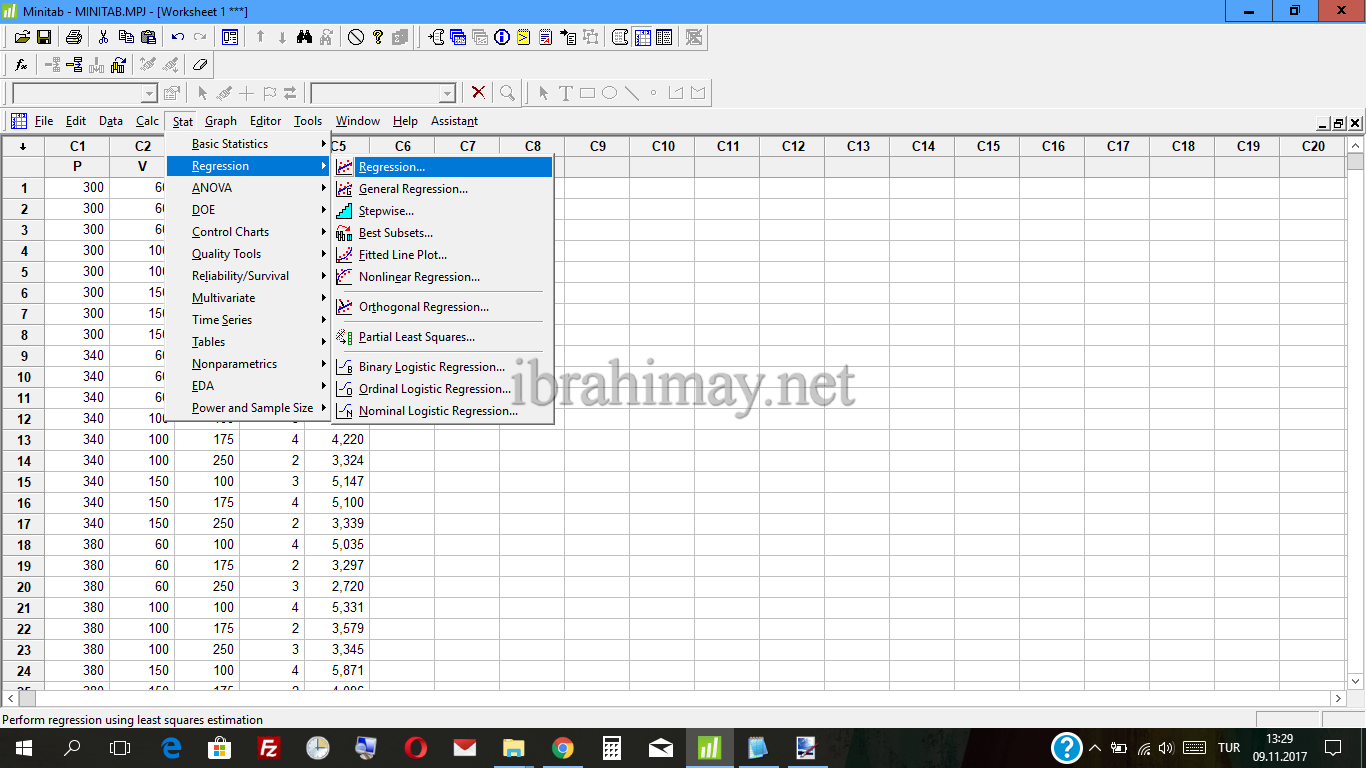
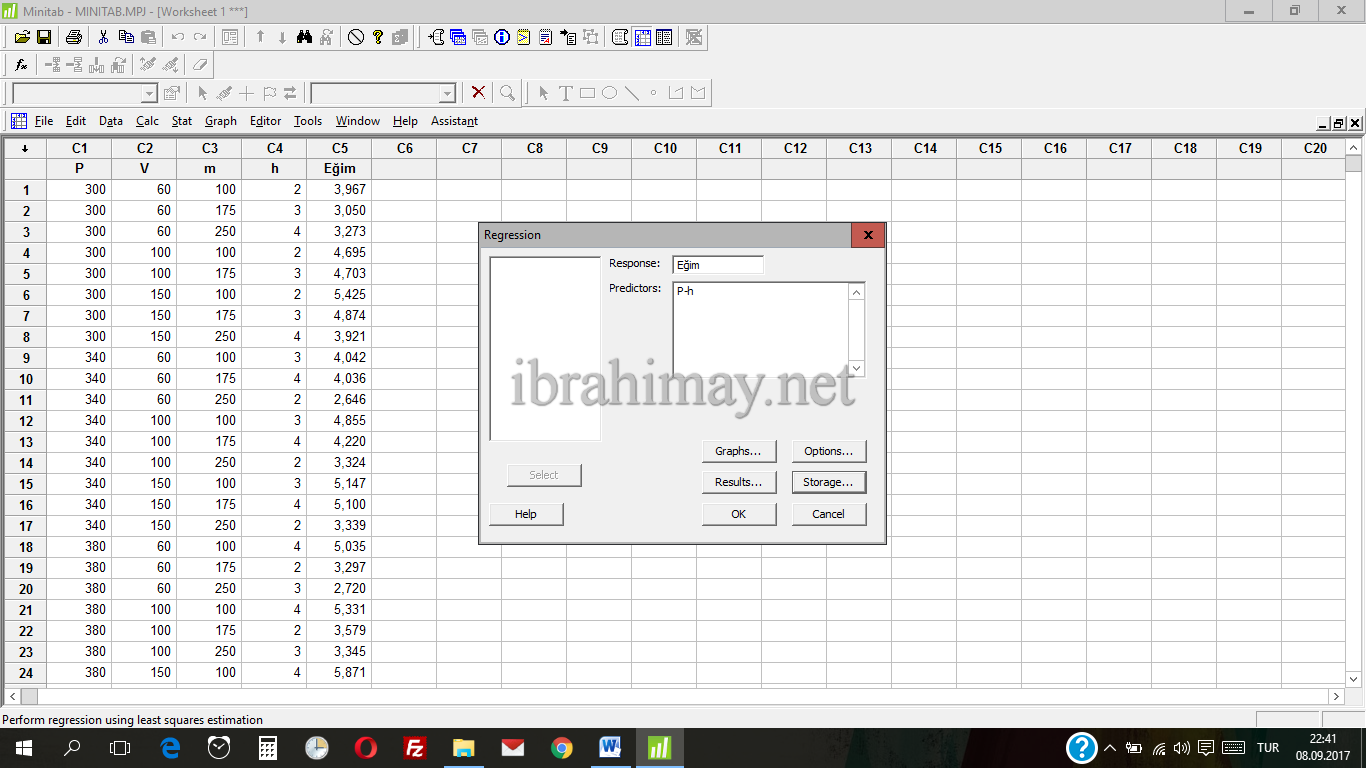
Menüden Stat–>Regression–>Regression adımlarını takip ederek aşağıdaki panomuza ulaşıyoruz. Response kısmına bağımlı değişkenimizi (Eğim); Predictors kısmına da bağımsız değişkenlerimizi (P,V,m,h) atıyoruz.

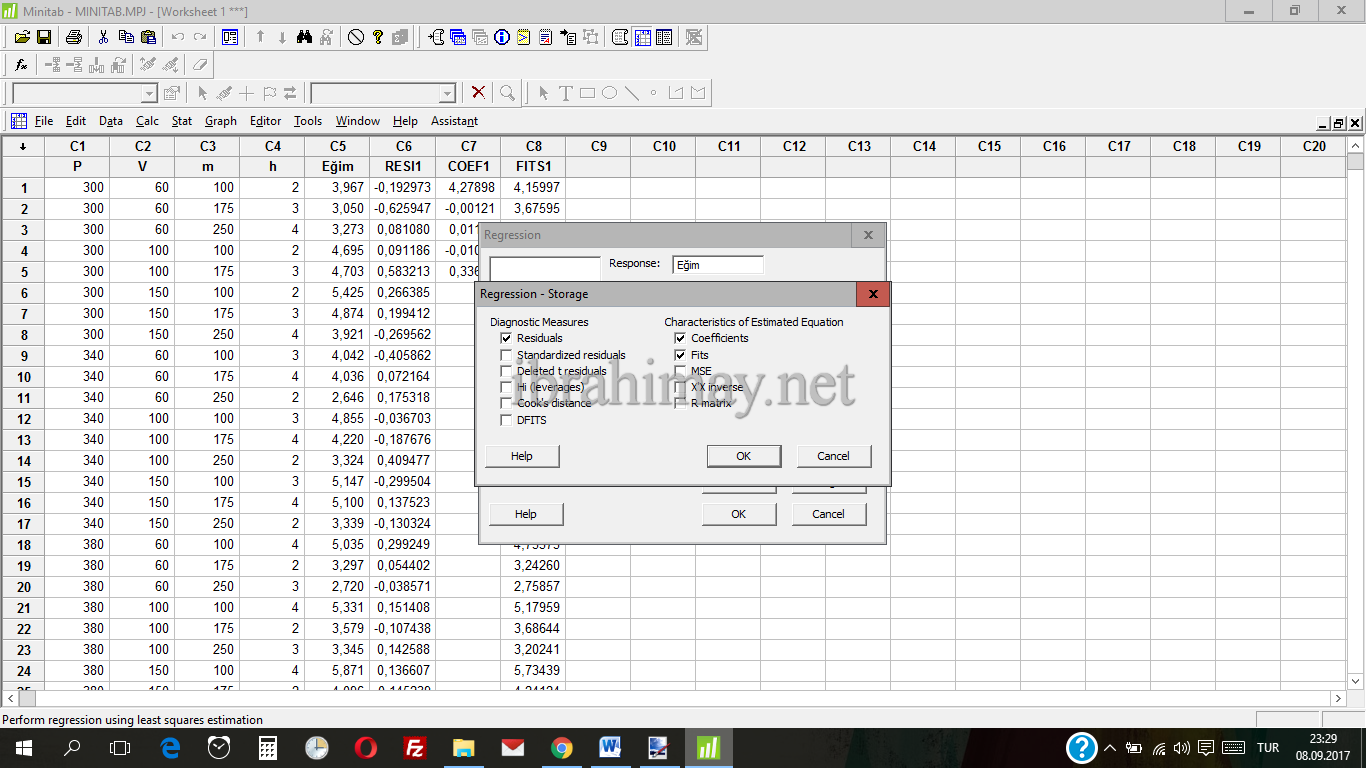
Daha sonra Storage… menüsünü tıklayarak regresyon denkleminin çıktısını ekrana basmak için

*Fits kutucuğunu;
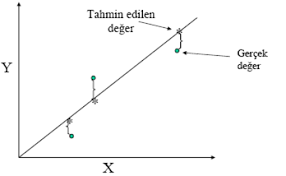
*Gerçek değer ile regresyon değeri arasındaki farkları ekrana basmak için Residuals kutucuğunu;
*Regresyon sabitlerini ekrana basmak için Coefficients kutucuğunu işaretliyoruz.

Bu seçimleri yaparak işlemi tamamladığımızda minitab tablosuna regresyon çıktısı, artıklar(residuals) ve regresyon sabitleri olmak üzere 3 sütun daha eklenmiş olacaktır. Eğer bunları ekrana basmak istemezseniz bu işlemi es geçin.

OK ve OK diyerek işlem sonucunu alıyoruz.

Session sayfamızda ise aşağıda görüldüğü gibi analiz sonuçlarımızı almış olmaktayız.

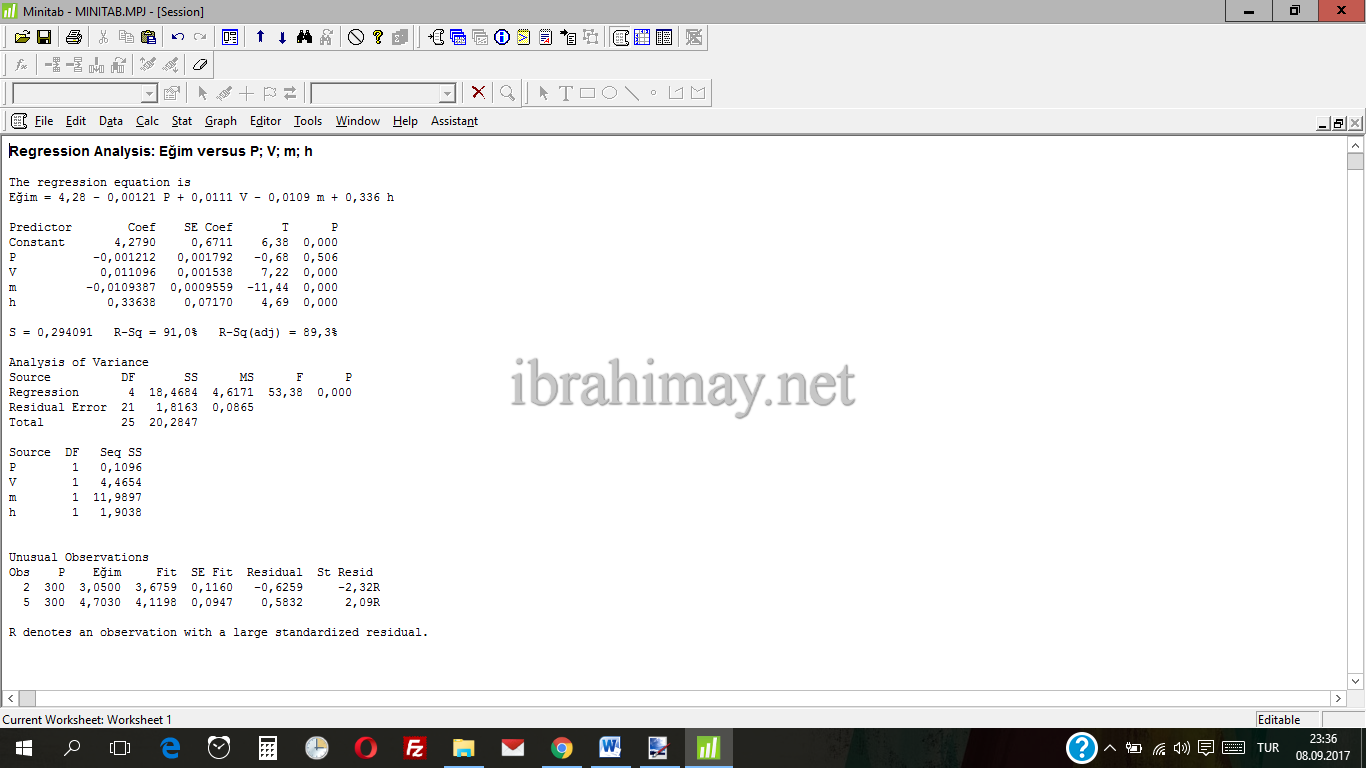
Çıktımızda “The regression equation is” başlığı altında regresyon denklemimiz verilmiş oluyor. Bizim sonucumuz şöyle:

Eğim = 4,28 – 0,00121 P + 0,0111 V – 0,0109 m + 0,336 h

Denklemimizde basınç (P) ve aşındırıcı sayfiyatı (m) negatif çarpanlı olduğuna göre bu iki değer arttıkça eğimin azaldığı, diğerleri arttığında ise eğimin arttığı yorumunu yapabiliriz.

Denklemden sonra bulunan katsayıların verildiği aşağıdaki tabloda bulunan P sütunudaki değerler, değişkenin istatiksel olarak anlamlı olup olmadığını anlamamıza yaramakta. Varyans analizlerinde de aynı yorum geçerli.

Predictor	Coef	SE Coef	T	P
Constant	4,2790	0,6711	6,38	0,000
P	-0,001212	0,001792	-0,68	0,506
V	0,011096	0,001538	7,22	0,000
m	-0,0109387	0,0009559	-11,44	0,000
h	0,33638	0,07170	4,69	0,000

P değeri 0,05’ten küçük ise değişkenimiz istatistiksel olarak anlamlı bir değişkendir, aksi durumda etkisiz olduğu kanaatine varabiliriz. Hipotezlerimizde anlamlılık için %95’i yeterli görmeyip %99 anlamlılık istersek 0,05 yerine 0,01 değerine göre yorum yapmamız gerekir.

Tablomuzda basıncın istatiksel olarak anlamsız olduğu kanaatine varıyoruz.

P (basınç)–>P (0,506)>0,05

Daha sonra ki satırımızda Rkare ve düzeltilmiş Rkare değerlerimiz veriliyor.

S = 0,294091   R-Sq = 91,0%   R-Sq(adj) = 89,3%

Regresyon denklemimiz deneyin %91’ini açıklıyor. Düzeltilmiş Rkare değerimiz %89’dur ve Rkareden çokta uzak değildir. Bu nedenle denklemimizin sağlıklı olduğunu söyleyebiliriz. Bazen Rkare yüksek olur ama düzeltilmiş Rkare çok düşüktür. O denklem sakat bir denklemdir, aklınızda olsun.

Daha sonra regresyon denklemine ait varyans analizi de veriliyor. P değeri 0,05’ten küçük ve dolayısıyla istatiksel olarak anlamlı bir denklemimiz var.

Analysis of Variance
Source	DF	SS	MS	F	P
Regression	4	18,4684	4,6171	53,38	0,000
Residual Error	21	1,8163	0,0865
Total	25	20,2847

Devamında “Unusual Observations” başlığı altında deney seti içinde olağandışı görülen deney satırlarına ait değerler verilmektedir. O satırları ister silin, ister deneyi yenileyin, isterseniz doğal karşılayın. Bana kalırsa doğal karşılayın. Zira o satırları silseniz başka değerleri olağandışı görmesi yüksek olasıdır. Deneyi yenilemek her zaman mümkün olmayabilir, mümkün olsa da sonuç muhtemelen değişmeyecektir. Bilginiz olsun yeter diye düşünüyorum.

Obs    P    Eğim     Fit      SE Fit  Residual  St Resid
2  300  3,0500  3,6759  0,1160   -0,6259     -2,32R
5  300  4,7030  4,1198  0,0947    0,5832      2,09R