MATLAB İle Yapay Sinir Ağı Uygulaması
Yapay Sinir Ağları hemen her alanda kullanılmaktadır. Bu çalışmada sayısal bir veri seti ile yapay sinir ağı eğitimi gerçekleştireceğiz.
Bu içerikte yapay sinir ağları ile ilgili teorik bilgilere girmeyi lüzumsuz görüyorum; zira ağda bolca bilgi bulabilirsiniz. Amacım yapay sinir ağını uygulamak isteyen arkadaşlara, yine uygulamalı bir örnek ile yardımcı olmaktır. Bu amaçla da MATLAB R2007a yazılımından yararlanacağım. Çalışmamız; verilerimizi ağa tanıtmak ile başlayacak, eğitim ile sürecek ve kontrol ile sonlanacaktır.
Konu için kullanacağım veri seti için Nazım SAKARYA ve Cevdet GÖLOĞLU imzalı “Taguchi Yöntemi İle Cep İşlemede Kullanılan Takım Yolu Hareketlerinin Ve Kesme Parametrelerinin Yüzey Pürüzlülüğüne Etkilerinin Belirlenmesi” başlıklı makaleden yararlandım. Bu makalenin dersimiz açısından hiçbir özelliği yok. Sadece gerçek verilerle dersi anlatmak için seçtim. Siz uygulamada, verilerinizin bir kısmı ile aşağıda anlatmaya çalıştığım şekilde eğitim yapıp, bir kısmınıda test için kullanmalısınız.
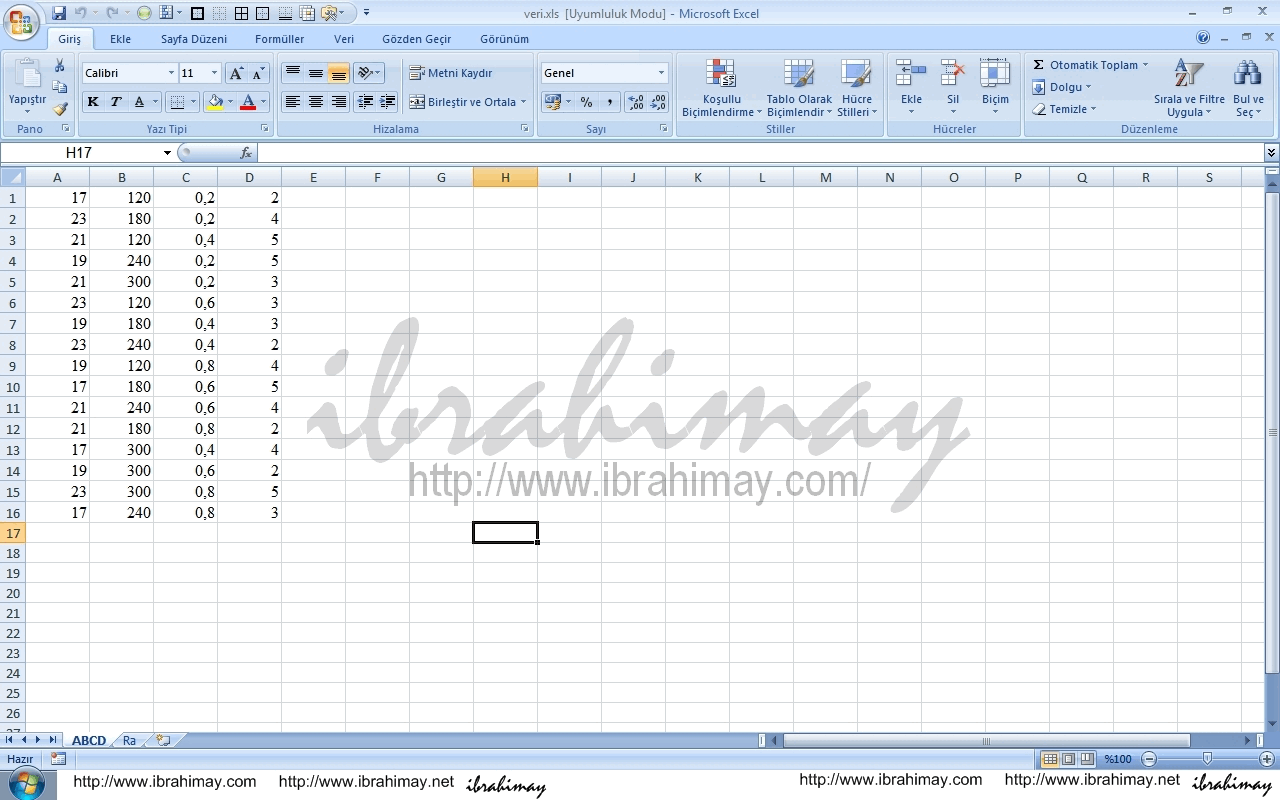
Bu bağlamda bağımlı ve bağımsız değişkenlerimiz şöyle (veri setimiz):
| Deney No | Bağımsız Değişkenler | Bağımlı Değişken* | |||
| Kesme Hızı(A) | İlerleme(B) | TalaşDerinliği
(C) |
KesiciYanal
Adımı (D) |
Yüzey Pürüzlülüğü(Ra) | |
| 1 | 17 | 120 | 0,2 | 2 | 1,68 |
| 2 | 23 | 180 | 0,2 | 4 | 1,80 |
| 3 | 21 | 120 | 0,4 | 5 | 2,41 |
| 4 | 19 | 240 | 0,2 | 5 | 4,13 |
| 5 | 21 | 300 | 0,2 | 3 | 3,74 |
| 6 | 23 | 120 | 0,6 | 3 | 1,79 |
| 7 | 19 | 180 | 0,4 | 3 | 2,77 |
| 8 | 23 | 240 | 0,4 | 2 | 2,97 |
| 9 | 19 | 120 | 0,8 | 4 | 3,38 |
| 10 | 17 | 180 | 0,6 | 5 | 4,24 |
| 11 | 21 | 240 | 0,6 | 4 | 4,03 |
| 12 | 21 | 180 | 0,8 | 2 | 3,42 |
| 13 | 17 | 300 | 0,4 | 4 | 5,98 |
| 14 | 19 | 300 | 0,6 | 2 | 2,07 |
| 15 | 23 | 300 | 0,8 | 5 | 4,45 |
| 16 | 17 | 240 | 0,8 | 3 | 5,03 |
*Çıktılarda Tek Yönlü Takım Yolu sonuçları kullanılmıştır.
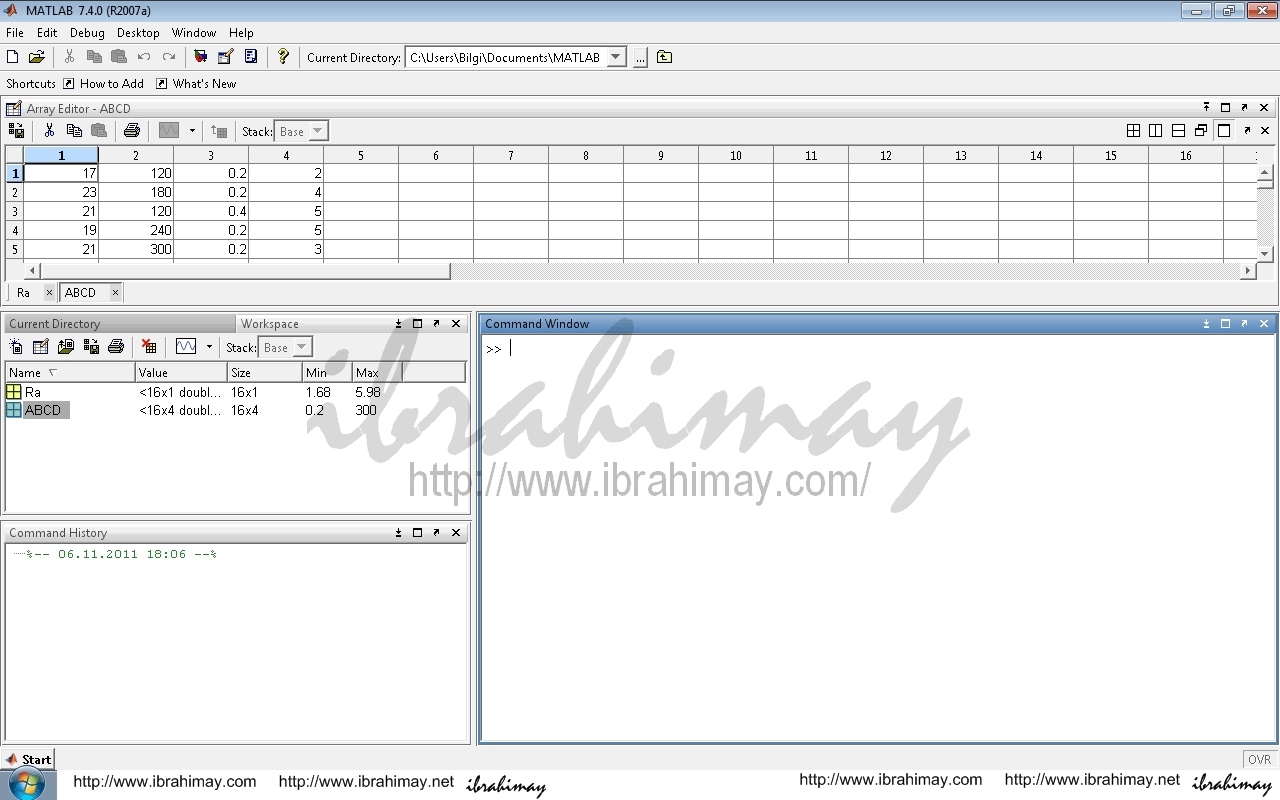
Öncelikle işlemleri birlikte yapacak isek aynı pencerelerde çalışmamızda fayda var. Zira bazı komutları sağdaki-soldaki gibi ifadeler ile tarif edersem karışıklık olmasın. Aşağıda MATLAB önyüzünü görüyorsunuz.
Yazılımınızı bu şekilde görmüyor iseniz;
Üst menüde ki Desktop altında ki şu komuları işaretleyin: Command Window; Command History ve Workspace.
Veya yine üst menüdeki Desktop altında ki Desktop Layout içinden Default yapın.
Netice de Command Window; Command History; Workspace dediğimde bu pencerelerin yerlerini bilin. Artık başlayabiliriz.
Verilerin Girilmesi
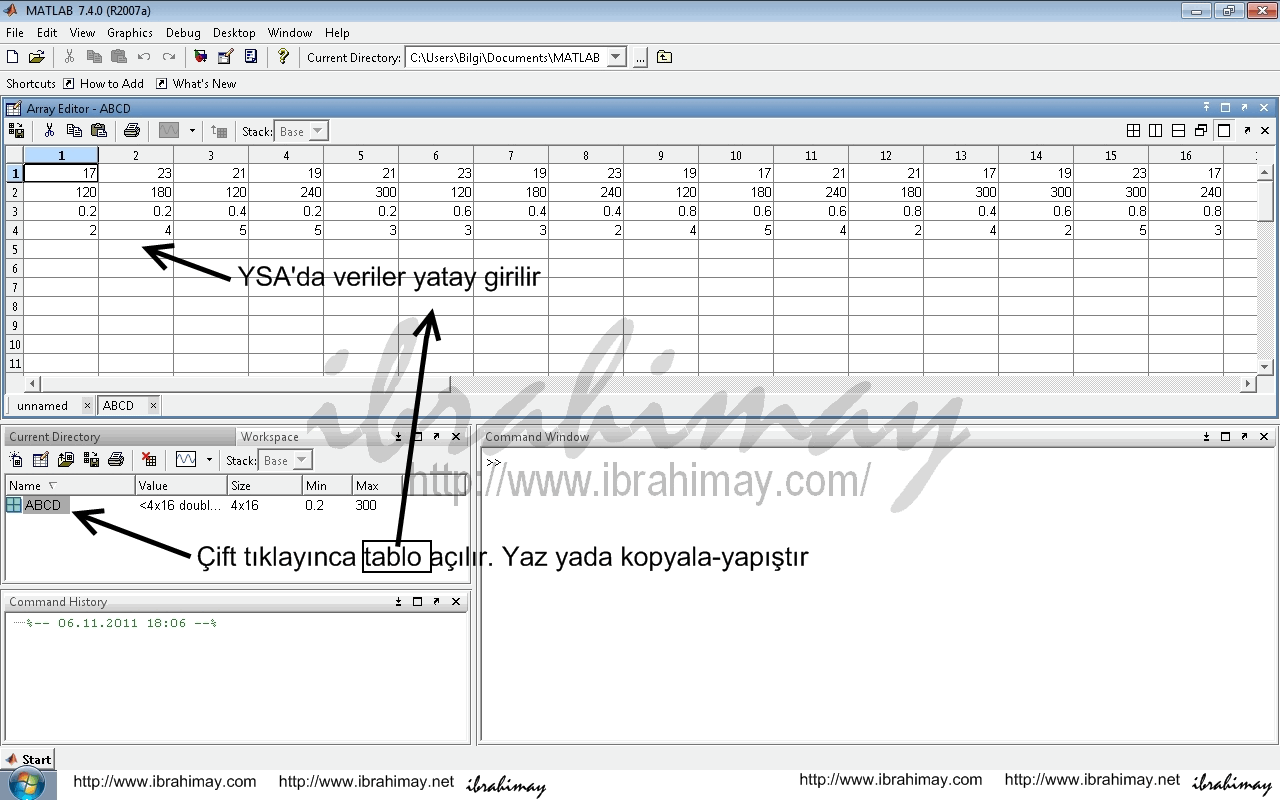
Öncelikle şunu bilmeliyiz ki, YSA’da veriler tanıtılırken yatay dizi kullanılır. Yani yukarıda ki veri setimizi şu şekle sokmuş olmalıyız:
| A | 17 | 23 | 21 | 19 | ….. | 19 | 23 | 17 |
| B | 120 | 180 | 120 | 240 | ….. | 300 | 300 | 240 |
| C | 0,2 | 0,2 | 0,4 | 0,2 | ….. | 0,6 | 0,8 | 0,8 |
| D | 2 | 4 | 5 | 5 | ….. | 2 | 5 | 3 |
| Ra | 1,7 | 1,8 | 2,4 | 4,1 | ….. | 2,1 | 4,5 | 5 |
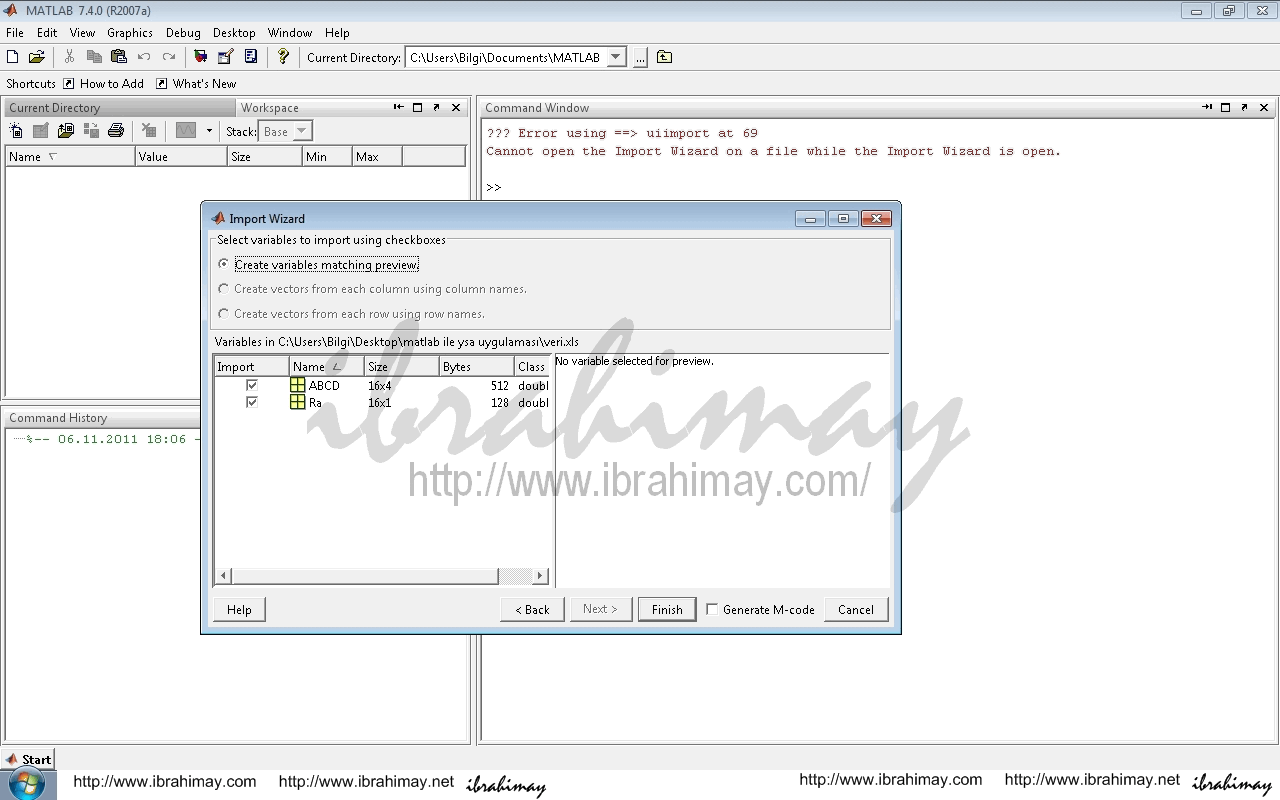
Diğer bir husus, bağımsız değişkenler (ABCD) bir tabloda, bağımlı değişken(ler) (Ra) bir tabloda olacak şekilde ayrı ayrı girilmelidir. Veriler Workspace’de New Variable ile tablolar açarak tek tek yazılabilir ancak sıkıcı ve uzun bir işlem olur.
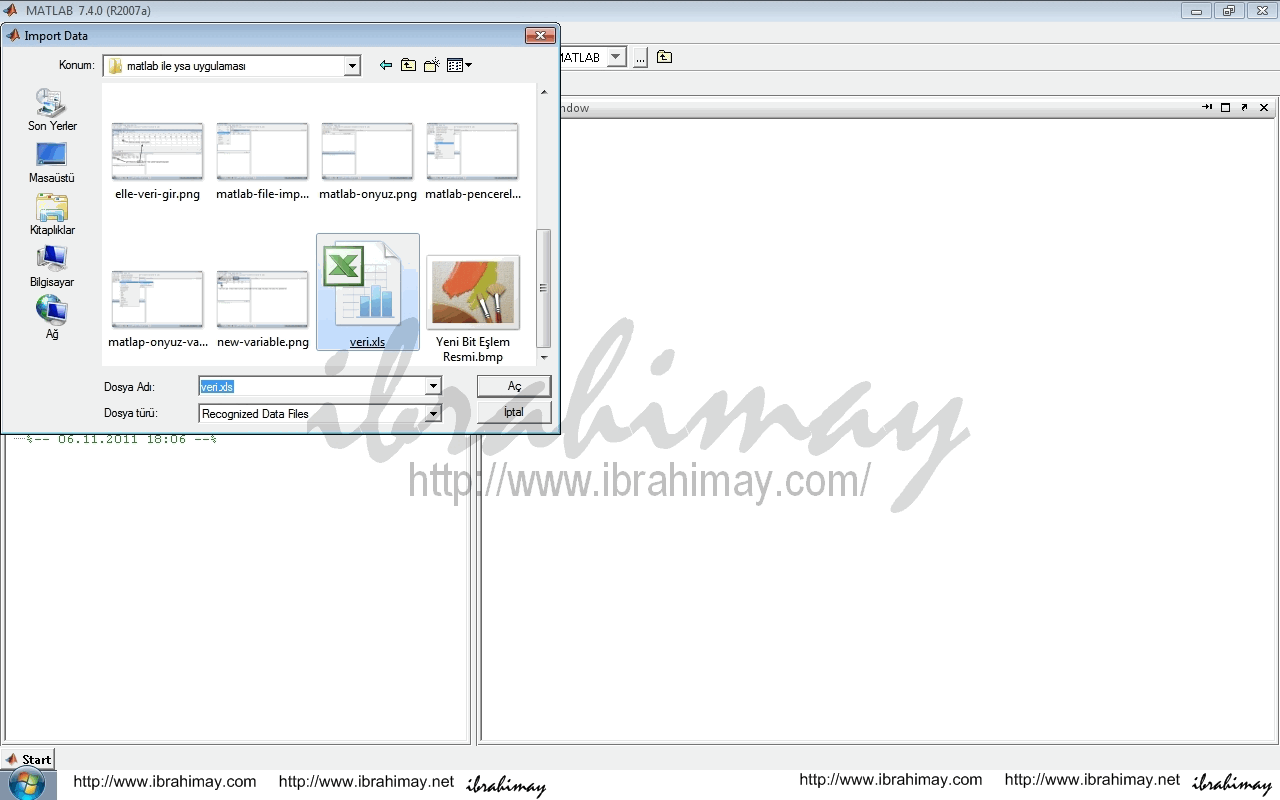
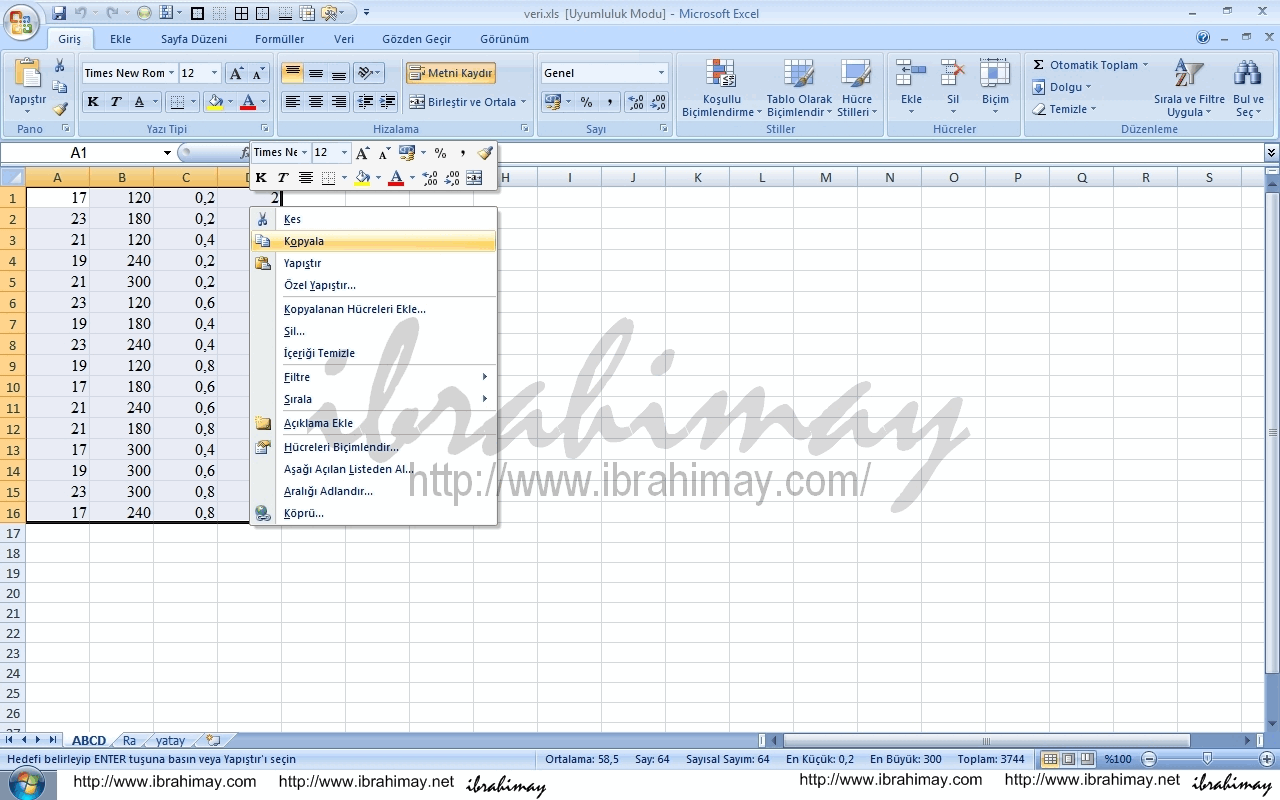
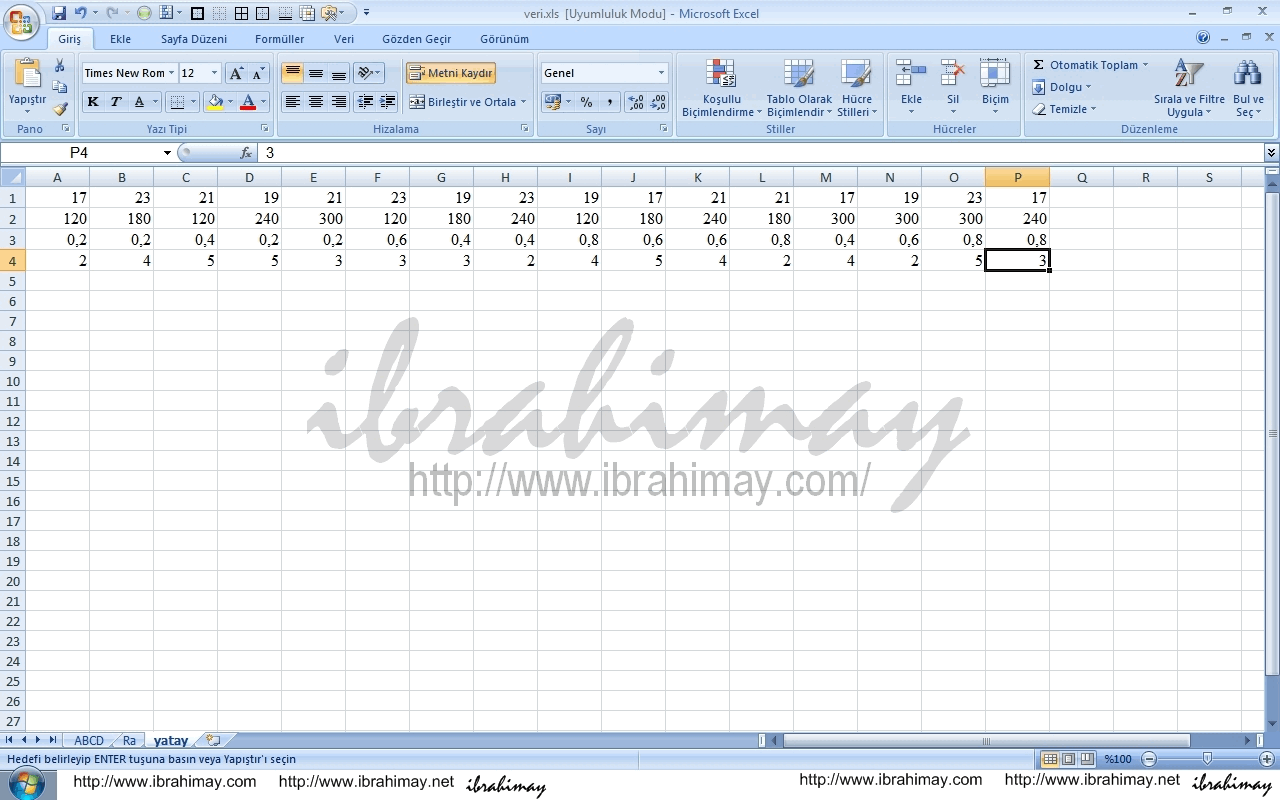
En iyisi ekselden aktarmaktır. Öncelikle bir Excel dosyası açın. Bir sayfasına girdileri, bir sayfasına çıktıları yazın ve 93-2007 excel (.xls) formatında kayıt edin. Sayfalara vereceğiniz isim tablolarınıza da isim olacaktır.
Daha sonra File–>import data ile ekselde hazır olan verileri matlaba aktarın.
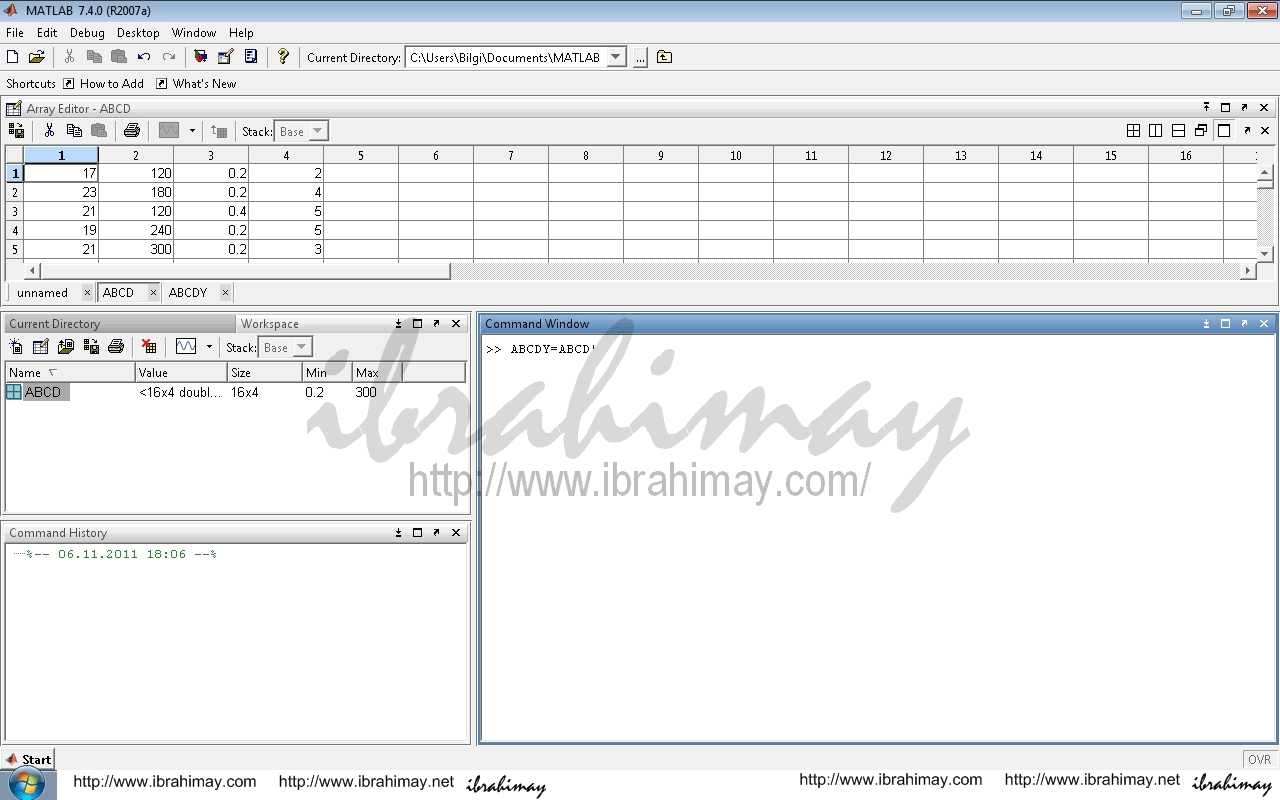
Verilerimiz alışılagelmiş dikey halde ise yatay hale getirmek gerek (transpoze);
Ekselde;
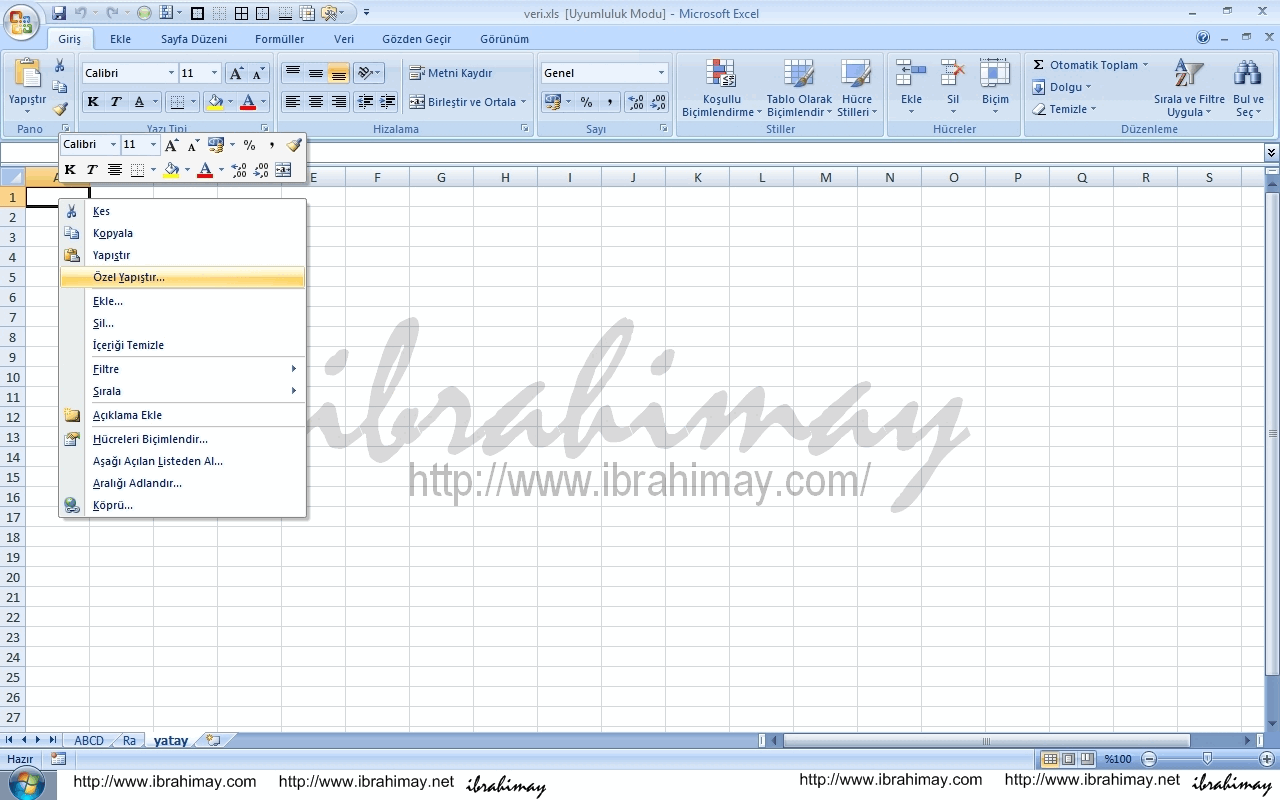
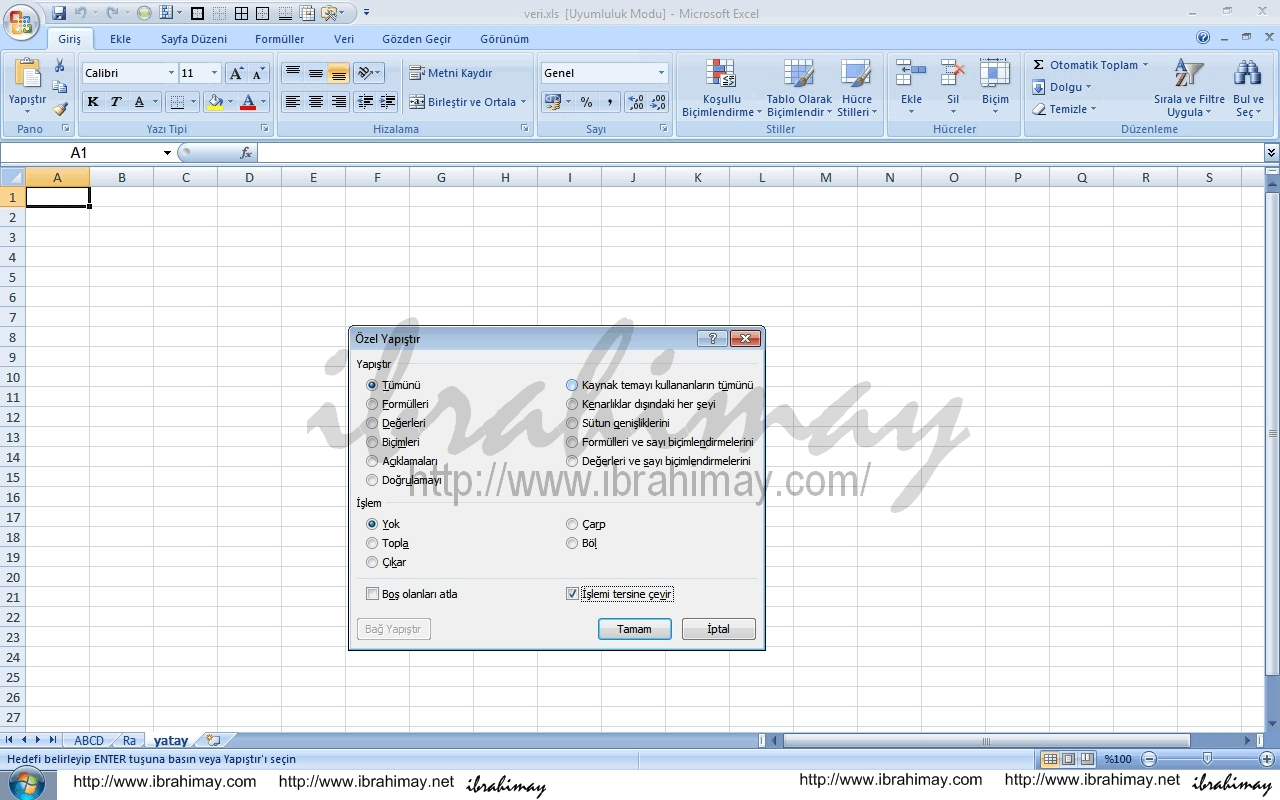
Yatay yazmak istediğiniz dikey verileri kopyalayın, sonra yapıştıracağınız yere sağ tık ile özel yapıştırı seçin, karşınıza çıkan pencerenin sağ alt köşesindeki “ işlemi tersine çevir” kutucuğunu işaretleyip tamam deyin.
Matlab’te
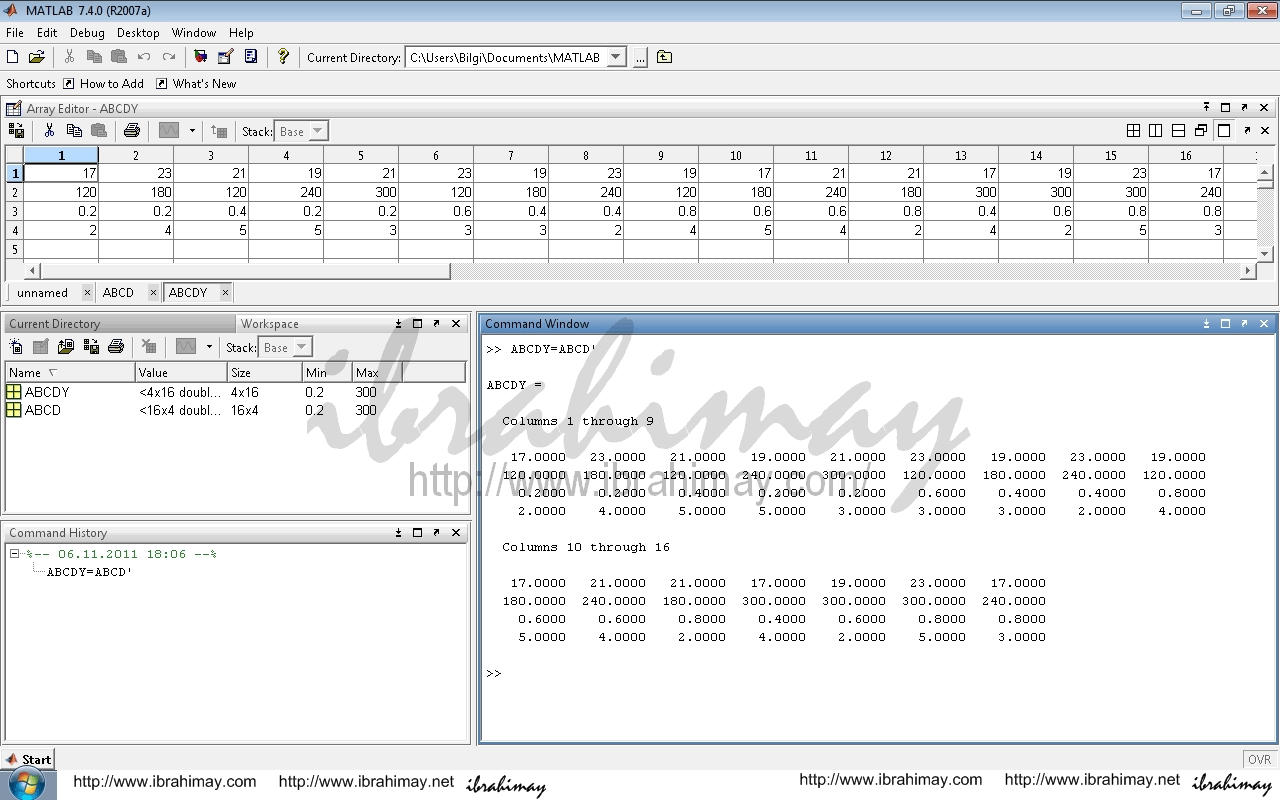
Tablomuz “ABCD” adını taşıyor ve dikey ise “Comman Window’a ABCD=ABCD’ yazın. Dikey tablom bozulmasın derseniz verilerinizi ABCDY gibi başka bir tabloda yatay hale getirebilirsiniz. Şöyle ki: ABCDY=ABCD’
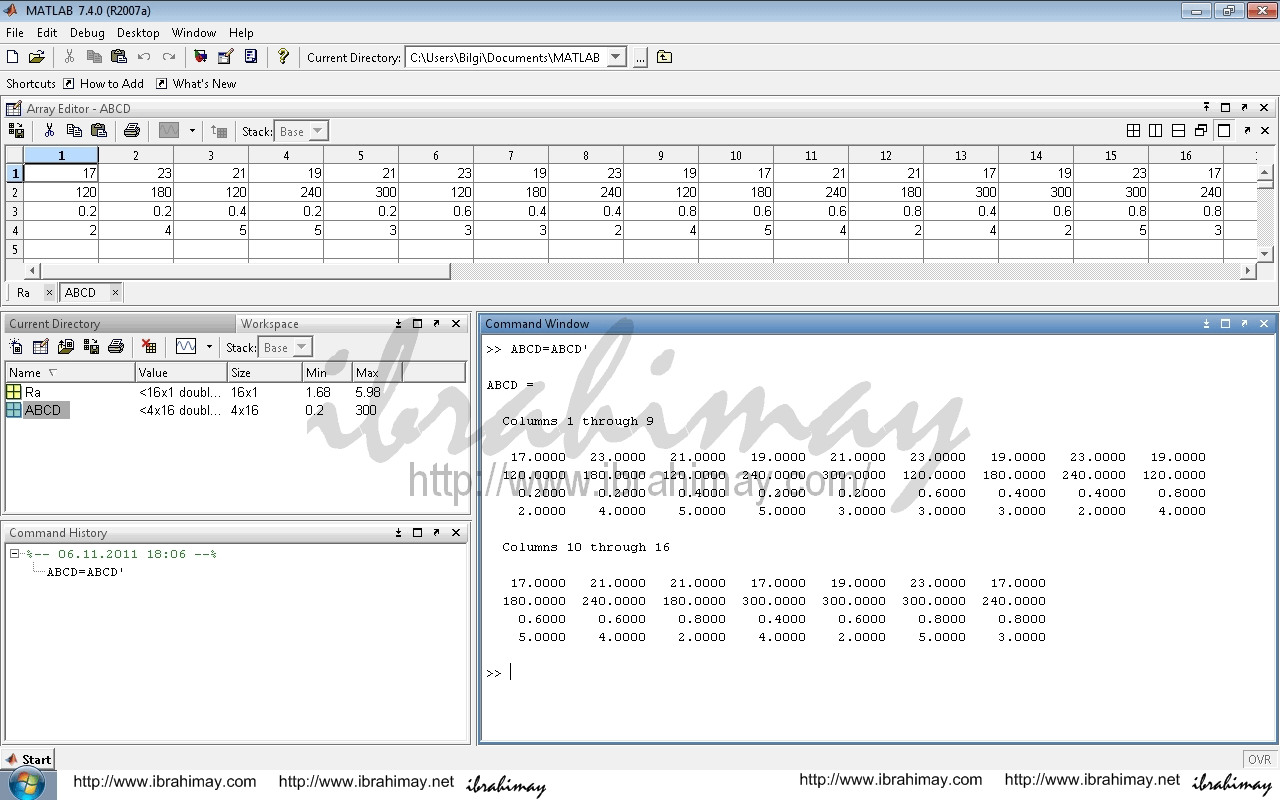
Veya aynı tabloyu yataya dönüştürerek değiştirin. ABCD=ABCD’
(Not: Üstteki kodu kopyala yapıştır ile alırsanız çalışmayabilir. Sağdaki ABCD’nin sonunda ki tek tırnaktır. Kılavyede Shift+2 ile elde edilmektedir. Yine yukarıdaki izahatları bağımlı değişken içinde uygulamalısınız. Yani örneğimizde ki Ra değerleri de yatay olmalı.)
Ağ Kurulumu Ve Eğitim
Verilerimizi girdik. Şimdi Yapay Sinir Ağı eğitimine başlayabiliriz. Öncelikle en basit eğitim olan “tek nöronlu doğrusal model” ile başlayalım. Bu eğitimin temsili resmi ve denklemi aşağıdaki gibidir.
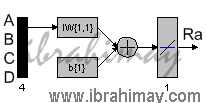 YSA = iw1*A + iw2*B + iw3*C + iw4*D + b1
YSA = iw1*A + iw2*B + iw3*C + iw4*D + b1
Burada ABC ve D olmak üzere 4 girişimiz var. Ağ, A bağımsızını rastgele seçtiği bir “iw1” sabiti ile, B bağımsızını “iw2”, C bağımsızını “iw3”, D bağımsızını da “iw4” sabiti ile çarparak “b1” hata oranı ile topluyor. Eğitim sonucu çıktımız olan Ra ile karşılaştırılıyor. Söz konusu döngü, en uygun çıktı için en uygun katsayılar belirlenene kadar sürdürülüyor. Elbette ki katsayıları değiştirme işlemi belli bir disiplin ile gerçekleştiriliyor (çıktı aranan değerden büyük ise katsayının veya katsayıların (veya sabitin) küçültülmesi gibi). Orasını fazla karıştırmayalım “,
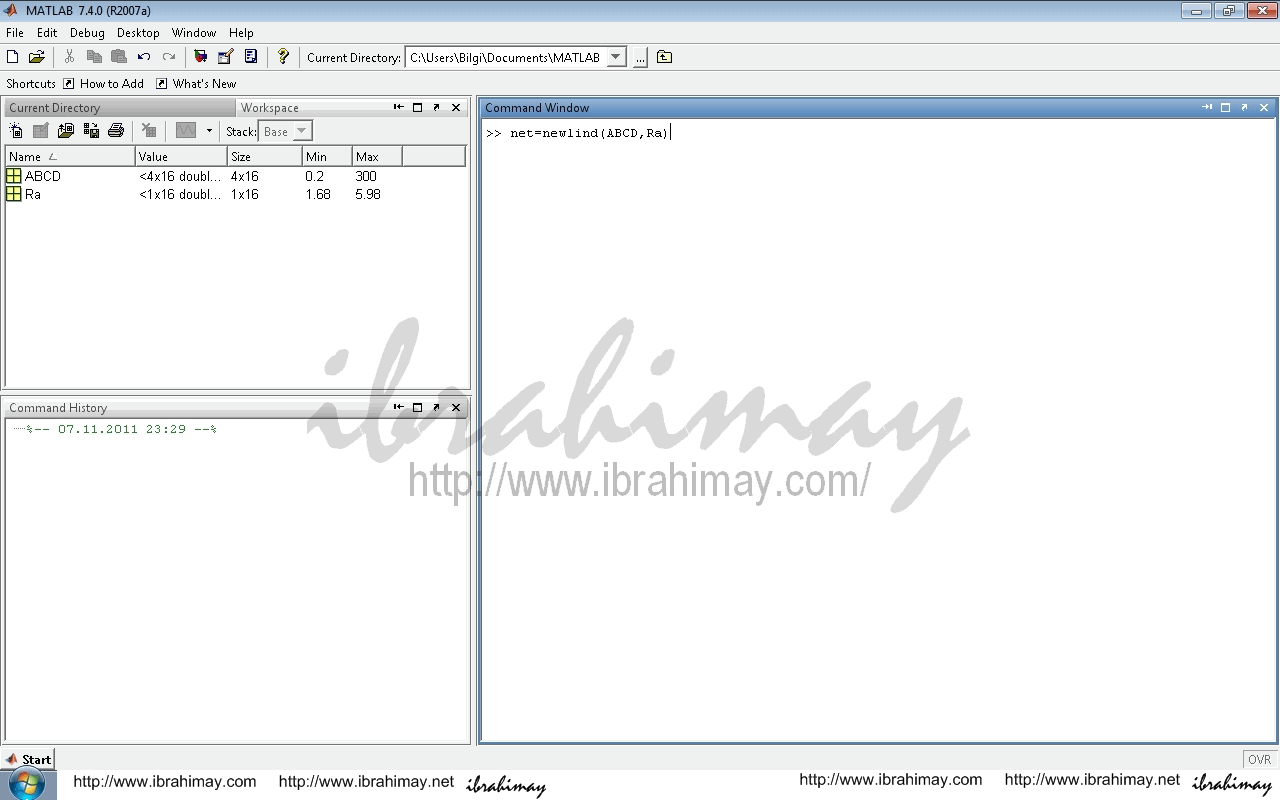
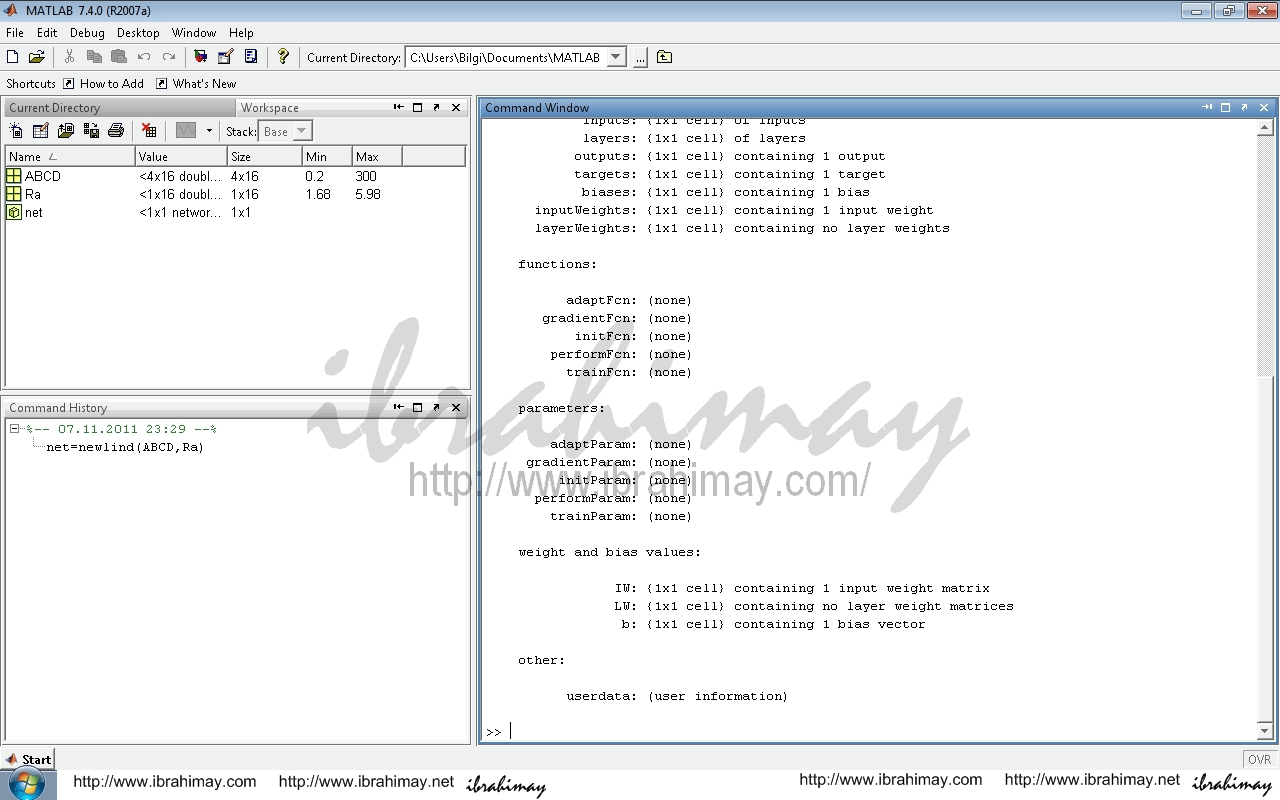
Bu eğitimin komutu net=newlind(girdi,çıktı) şeklindedir. Bizim girdilerimiz ABCD, çıktılarımız Ra isimli veriler olduğu için kullanacağımız komut net=newlind(ABCD,Ra) olacaktır. Bu komutu girdiğimizde ağımız eğitilmiş olur.
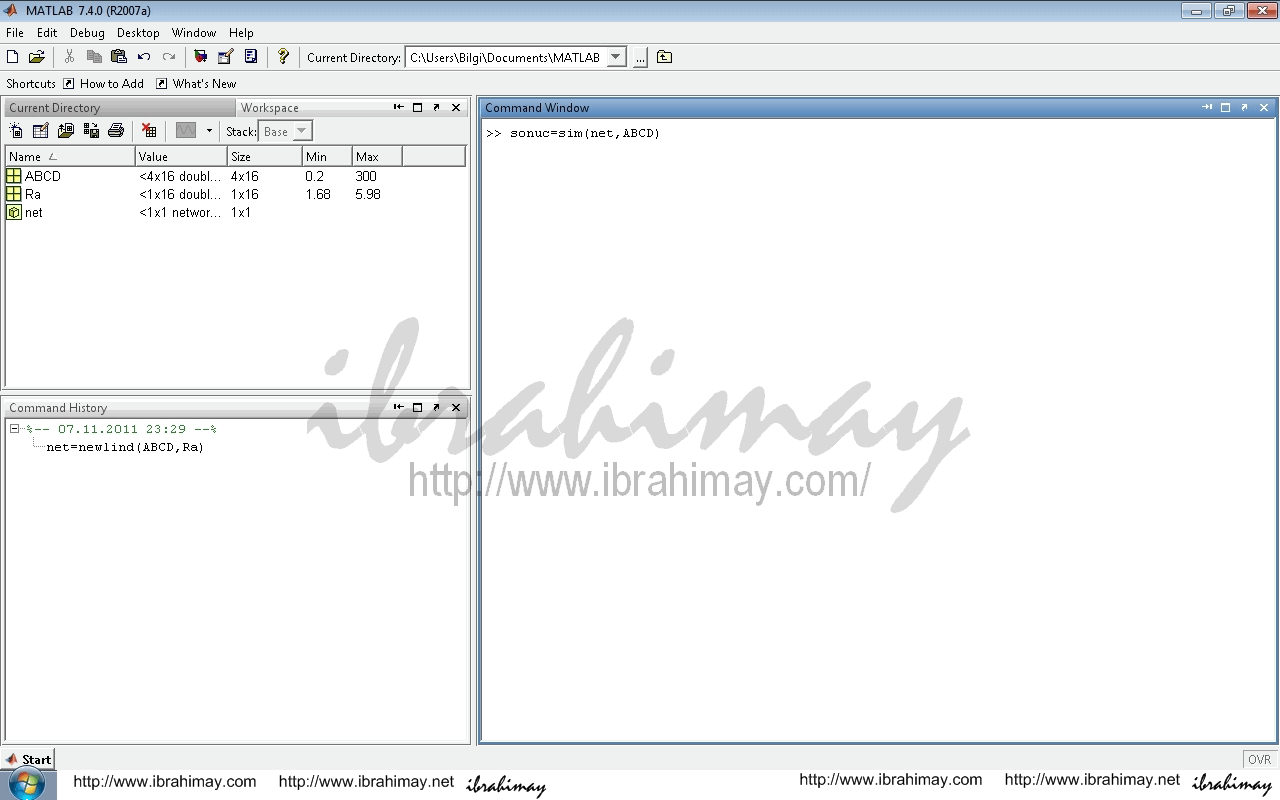
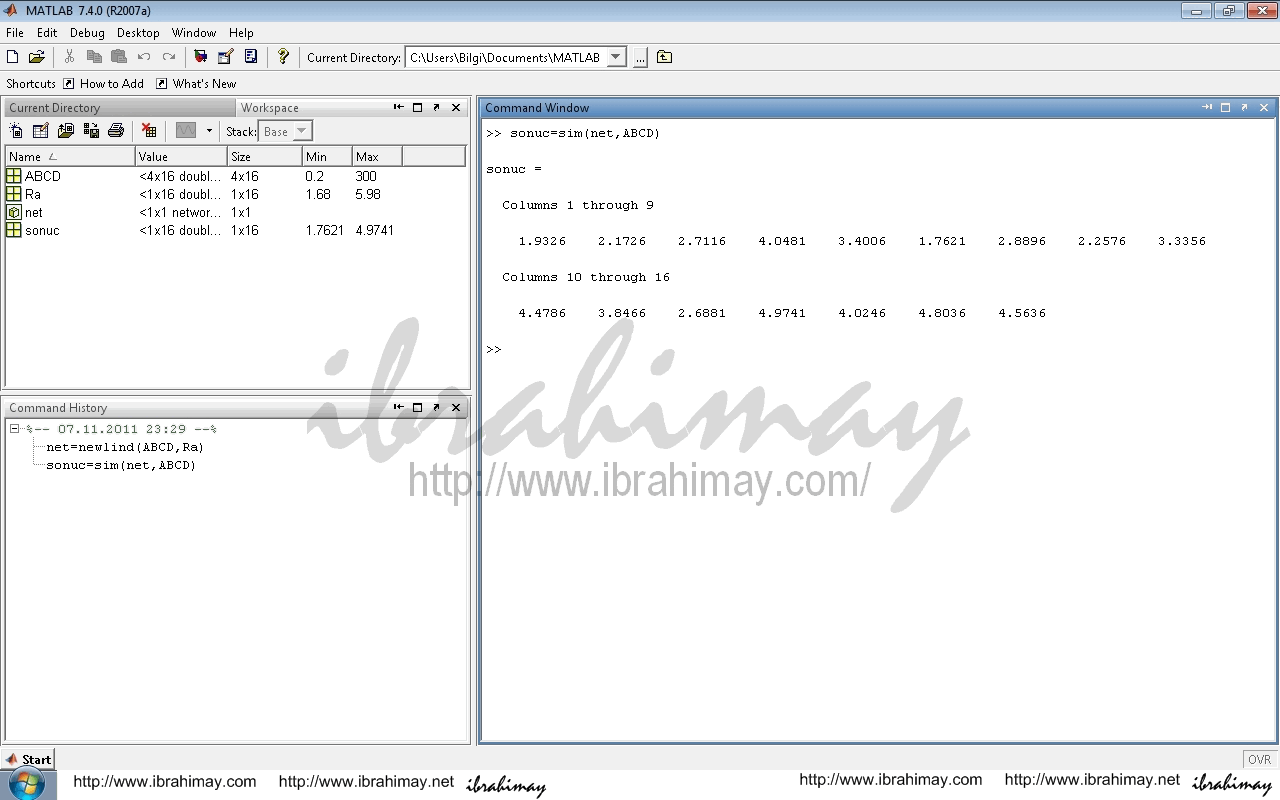
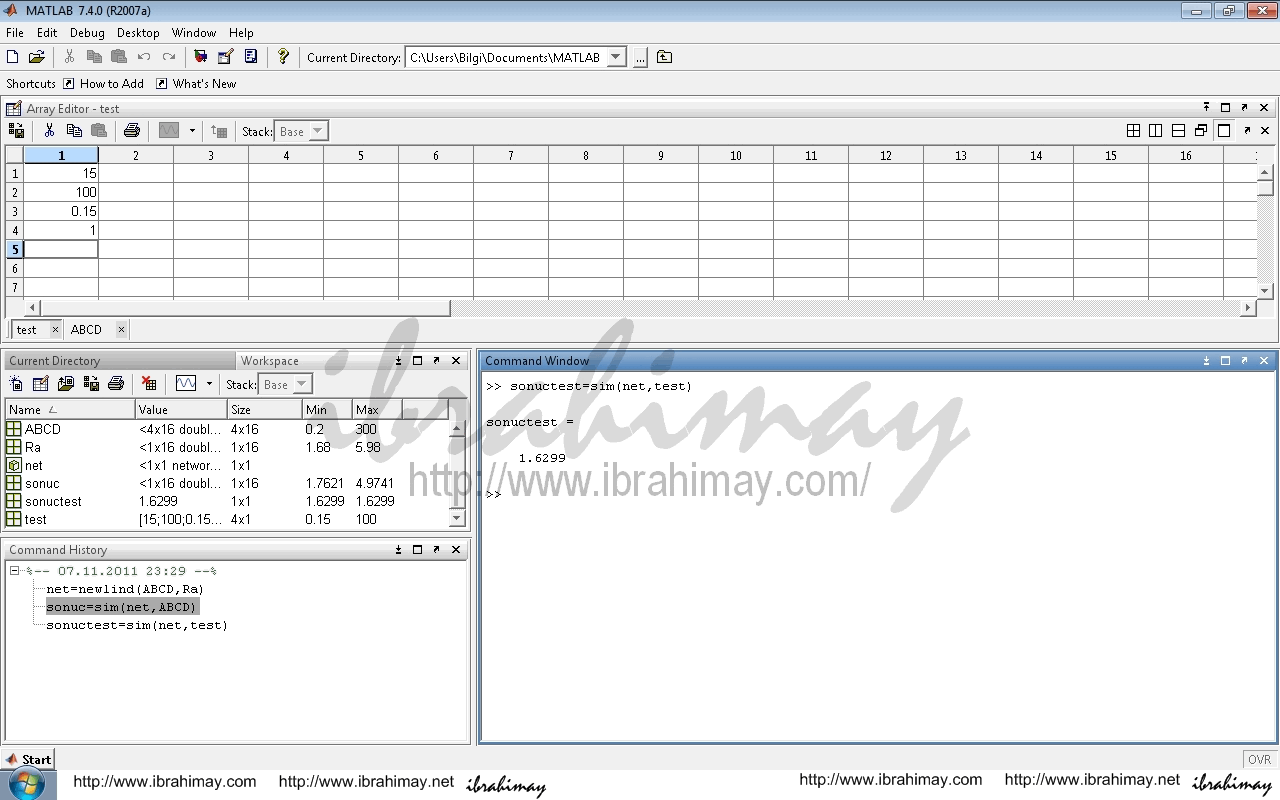
Bu ağ ile edilen sonuçları görmek için sonuc=sim(net,ABCD) komutunu kullanırız.
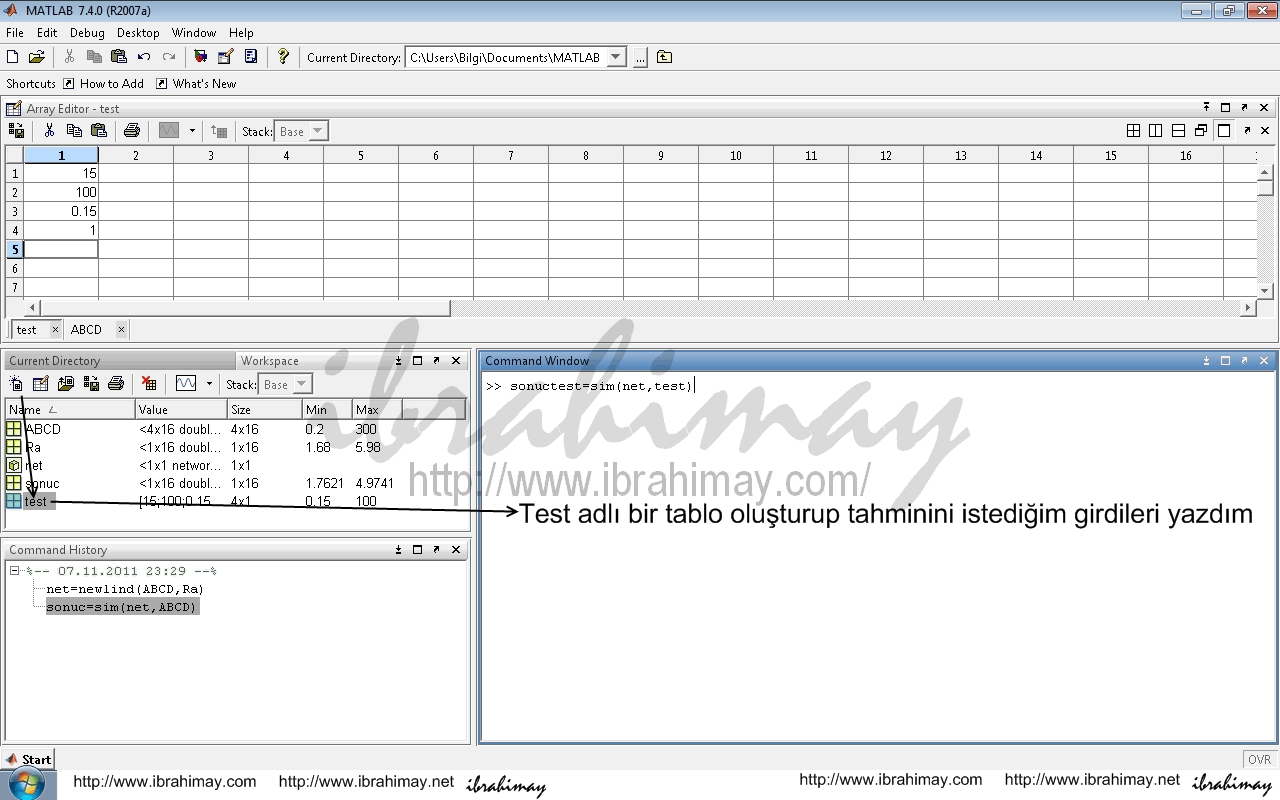
Veya eğitimin başarısını ölçmek için, eğitim esnasında kullanılmamış başka değerlerin sonucuna da bakabilirsiniz.
Mesela test adlı bir tablo oluşturup girdilerimizi tanıtalım ve sonuctest=sim(net,test) ile sonucu (tahmini) alalım.
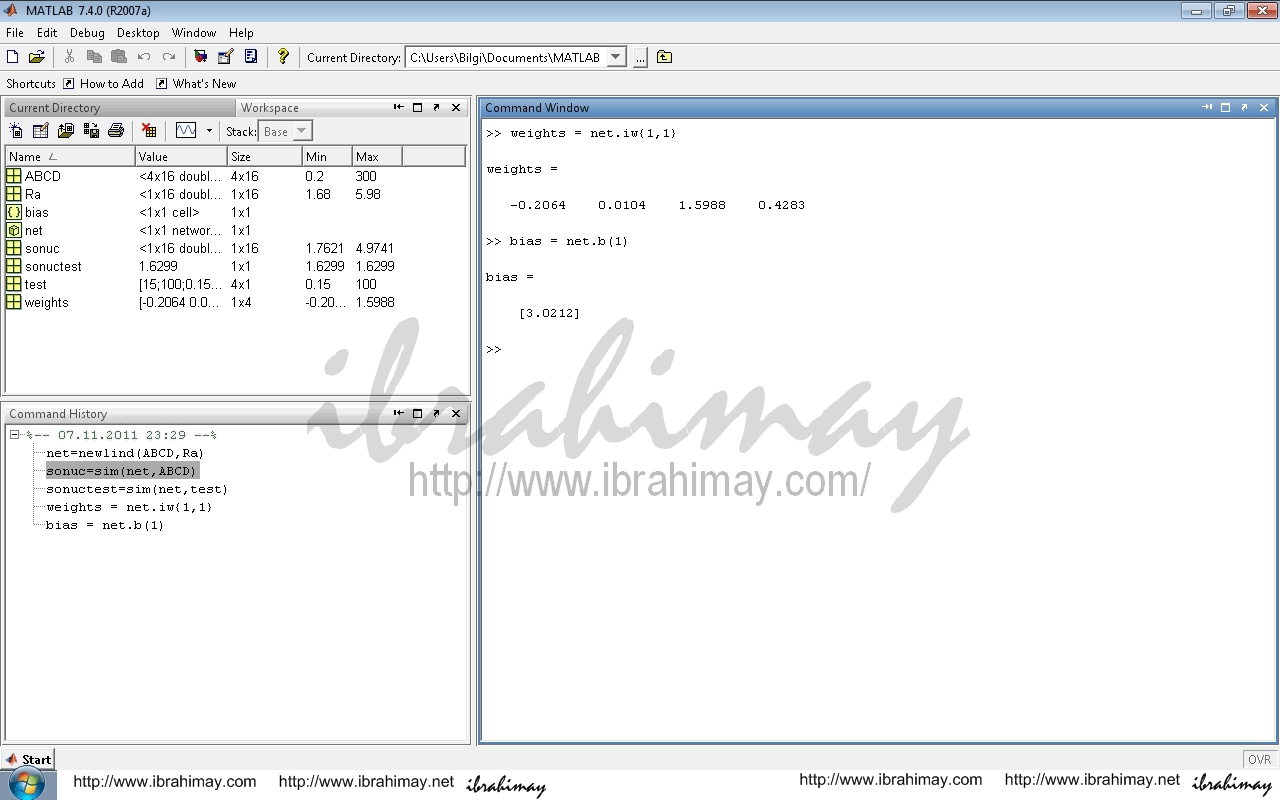
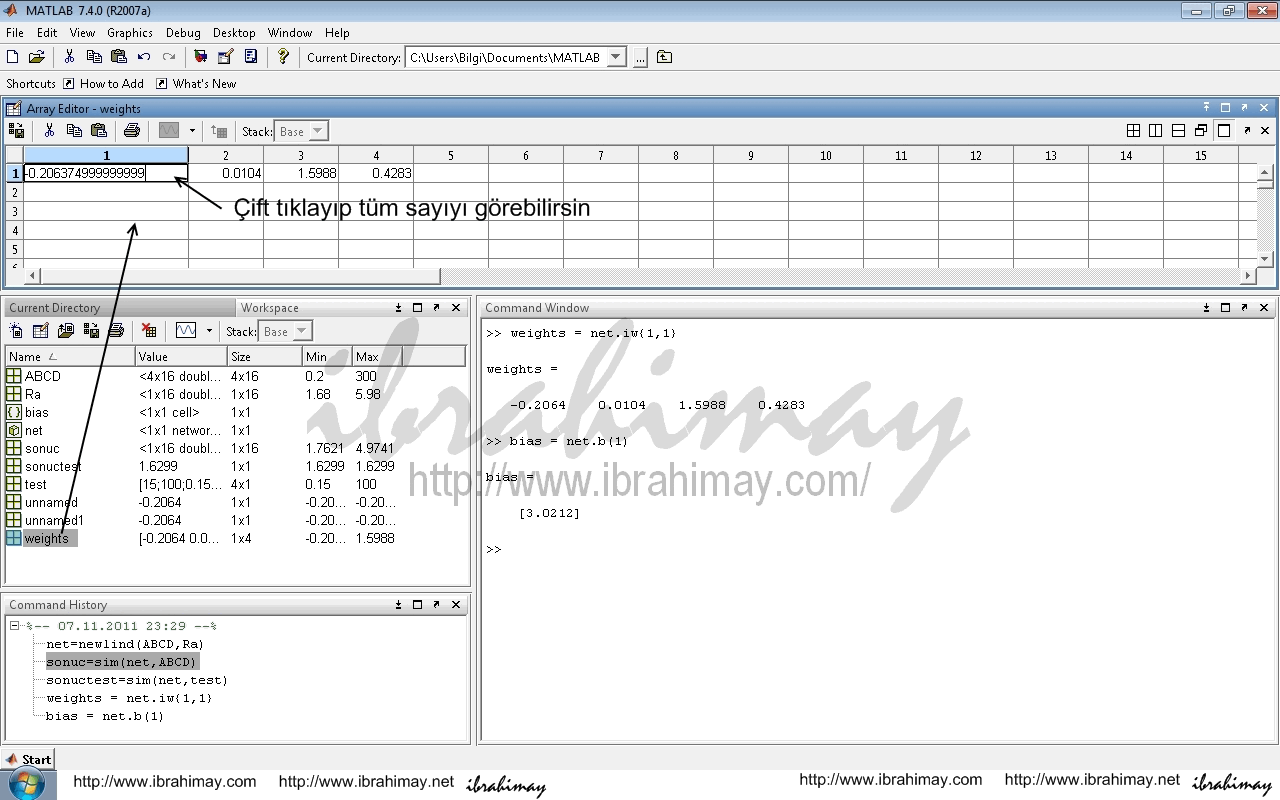
Bu eğitim ile elde edilen sonuçlar regresyon ile alacağınız sonucun aynısınıdır. Nasıl ki regresyonda bağımsız değerler birer katsayı ile çarpılıp bir hata değeri ile toplanıyorsa, bu eğitim de de aynı denklem söz konusudur. Tek fark sabitlerin bulunma yöntemidir. Ağın çarpanlarını öğrenmek için weights = net.iw{1,1}, sabiti öğrenmek içinde bias = net.b(1) komutunu kullanalım. (Veya bias = net.b{1} weights = net.iw{1})
Örneğimizde elde ettiğimiz sonuç;
weights = -0.2064 0.0104 1.5988 0.4283
bias = 3.0212
şeklindedir. Bu bağlamda sinir ağı çıktıyı şu şekilde hesaplamaktadır:
-0.2064*A+0.0104*B+1.5988*C+0.4283*D+3.0212
Birinci satır için örneklersek;
-0.2064*17+0.0104*120+1.5988*0.2+0.4283*2+3.0212=1,9367
YSA çıktımız 1.9326 iken neden aynı sonucu bulmadık. Çünkü katsayıların sadece virgülden sonra ki 4 hanesini kullandık. Gerçekte bu katsayıların virgülden sonra ki kısmı daha uzundur. Weights ve bias tablolarında bunu görebilirsiniz.
Sabitlerimizde virgülden sonra 6 haneyi kullanırsak formülüz şu olur:
-0.206374*A+0.010363*B+1.59875*C+0.42825*D+3.02125
-0.206374*17+0.010363*120+1.59875*0.2+0.42825*2+3.02125=1,9327
Denklemi kısa tutmak için bu şekil bize yeter. Sabitleri birebir kullanırsak YSA çıktısını birebir elde ederiz. Eğer regresyon hesabı yaparsanız aynı sabitlere çok çok yakın değerler elde ettiğinizi göreceksiniz. Yapay sinir ağının en basit halini kısaca görmüş olduk. Şimdi bir adım ileri giderek ileri beslemeli çok katmanlı bir ağ eğitimi yapalım.
İleri Beslemeli Çok Katmanlı Ağ
Bu eğitimin komutu newff’dir. Bu eğitimin temsili ve denklemi için basit bir örnek aşağıdaki gibidir. İlgili temsil eğitim ağımıza göredir.
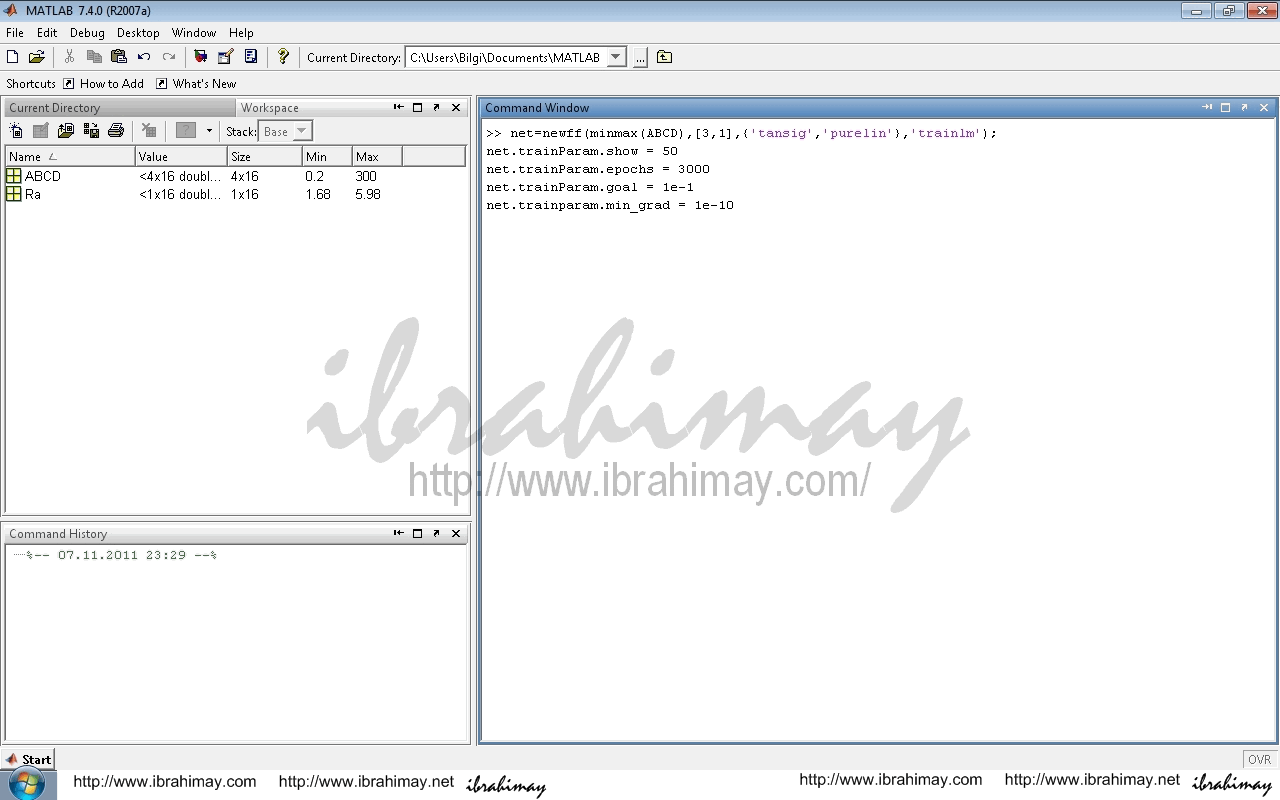
net=newff(minmax(ABCD),[3,1],{‘tansig’,’purelin’},’trainlm’);
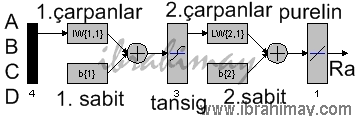
Adım adım anlatmaya çalışayım. A,B,C,D girişleri rastgele iw katsayıları ile çarpılıp b1 sabiti ile toplanıyor. İlk derste anlattığım gibi (regresyon denklemi gibi).Elde edilen sonuç 3 nöronlu tansig denkleminin 1. nöronundan geçiriliyor. Tansig fonksiyonu 2/(1+exp(-2*n))-1 şeklindedir. Burada exp doğal logaritmayı (e) ifade etmektedir. Sayısal örnekte göreceğiz. Tansig yerine logsig(n) = 1 / (1 + exp(-n)) gibi farklı denklemler ile eğitim yapılabilir. Ancak YSA’da ki her denklem bu tip sayısal işlemlere uymaz. Mesela hardlim(n) ( 1 if n>=0) denklemi var ki çıktı’nın 0’dan büyük veya eşit olmasına göre sonucu 1 varsayıyor. Devam edelim. Yeni sonuçlar bir sonraki adımda iw2 katsayıları ile çarpılıp b2 sabiti ile toplanarak purelin fonksiyonuna sokuluyor. Purelin fonksiyonu n=n’dir, yani çıktının kendisidir. Purelin yerine tansig, logsig vb kullanabilir veya deneyebilirsiniz. En sonda ki trainlm komutu ise Levenberg-Marquardt geri yayılım algoritmasının kullanılacağını ifade eder. Bundan başka trainbfg, trainbr, traincgb, traincgf, traincgp, traingd, traingda, traingdm, traingdx, trainoss, trainrp, trainscg, trainb, trainc, trainr gibi algoritmalar mevcuttur.
Ağı daha çok katmanlı ve daha çok nöronlu yaparsak sayısal işlem muazzam derecede artar ve ben size anlatamam. Siz çalışmalarınızda uygularsınız o başka. Mesela;
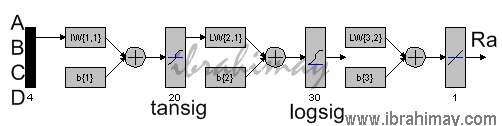
net=newff(minmax(ABCD),[20,30,1],{‘tansig’,’logsig’,’purelin’},’trainlm’);
Burada bağımsızlar katsayılar ile çarpılıp sabit ile toplanıyor. 20 nöronlu tansig denkleminin 1 nöronundan geçiyor. Bu diğer katsayılar ile çarpılıp, toplanıp 30 nöronlu logsig denklemine sokulup purelinden çıktı alınıyor. Birazdan net=newff(minmax(ABCD),[3,1],{‘tansig’,’purelin’},’trainlm’); işleminin sonucunu sayısal olarak değerlendirdiğimde ne demek istediğimi anlayacaksınız. Ondan önce ağı eğitirken bazı yardımcı kodlar kullanmamız gerekebiliyor.
net.trainParam.show = 5; komutu eğitimin ilerleyişini kaç döngüde bir göstereceğini ifade eder.
net.trainParam.epochs = 300; komutu eğitimin kaç döngüye kadar yapılacağını ifade eder. Yukarıda hesaplama hakkında dilim döndüğünce bir şeyler anlatmıştım. O anlatım bir döngüdür. Aynı işlemi azami kaç kere yapsın sorusuna burada 300 cevabını vermiş oluyoruz ki eğitim başarılı olmaz ise ya işlemi yenileriz veya bu döngü sayısını arttırırız. Döngü sayısını arttırmak çalışmayı bozmazsa da çok fazla olursa eğitim ezberlemeye dönüşür ve eğitim dışında ki yeni verilerin kontrolü çok başarısız olabilir.
net.trainParam.goal = 1e-5; Bu komut, hata karelerinin toplamı kaç olduğunda döngü sonlansın sorusuna cevaptır. Eğer yukarıda verdiğimiz azami 300 döngü sonunda bu hata oranına ulaşılamazsa eğitim başarısız demektir.
net.trainparam.min_grad = 1e-10; Ağın performans değeri. Düşük olursa istediğimiz MSE değerine ulaşamayabiliriz, bu anlamda yüksek tutmakta fayda var.
Şimdilik bunlar yeter. Benzer yardımcı kodları MATLAB Help’ten öğrenebilirsiniz.
Son olarak eğitime aşağıdaki komutla başlarız;
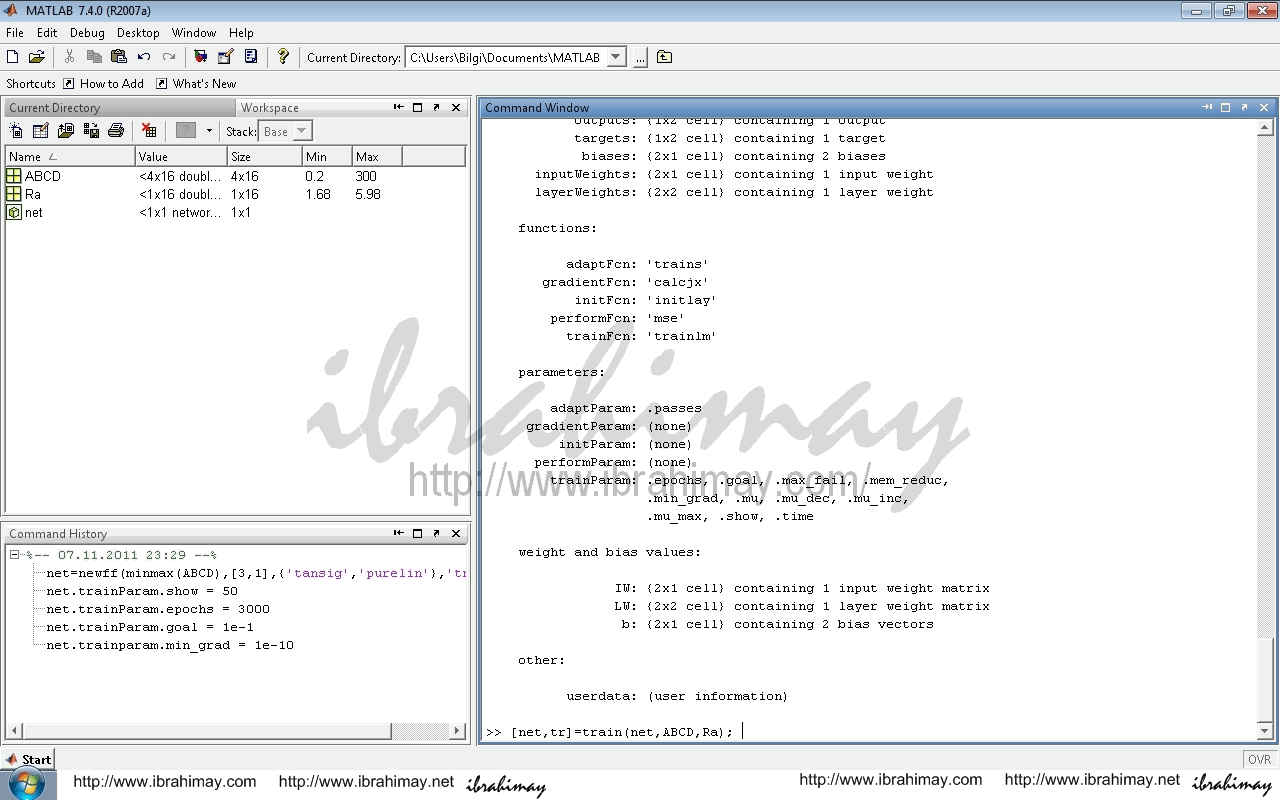
[net,tr]=train(net,ABCD,Ra);
Elimizde ki veriler ile eğitime başlayalım. Aşağıda ki kodlarımda ki sayılar genel uygulamalara göre farklıdır. Veri sayımın azlığından ziyade dersi anlatabileceğim nöron sayısı ile eğitimi tamamlama şansım zayıf. Bu nedenle hedef hata kareleri toplamını ve bazı değerleri yüksek tuttum.
net=newff(minmax(ABCD),[3,1],{‘tansig’,’purelin’},’trainlm’);
net.trainParam.show = 50
net.trainParam.epochs = 3000
net.trainParam.goal = 1e-1
net.trainparam.min_grad = 1e-10
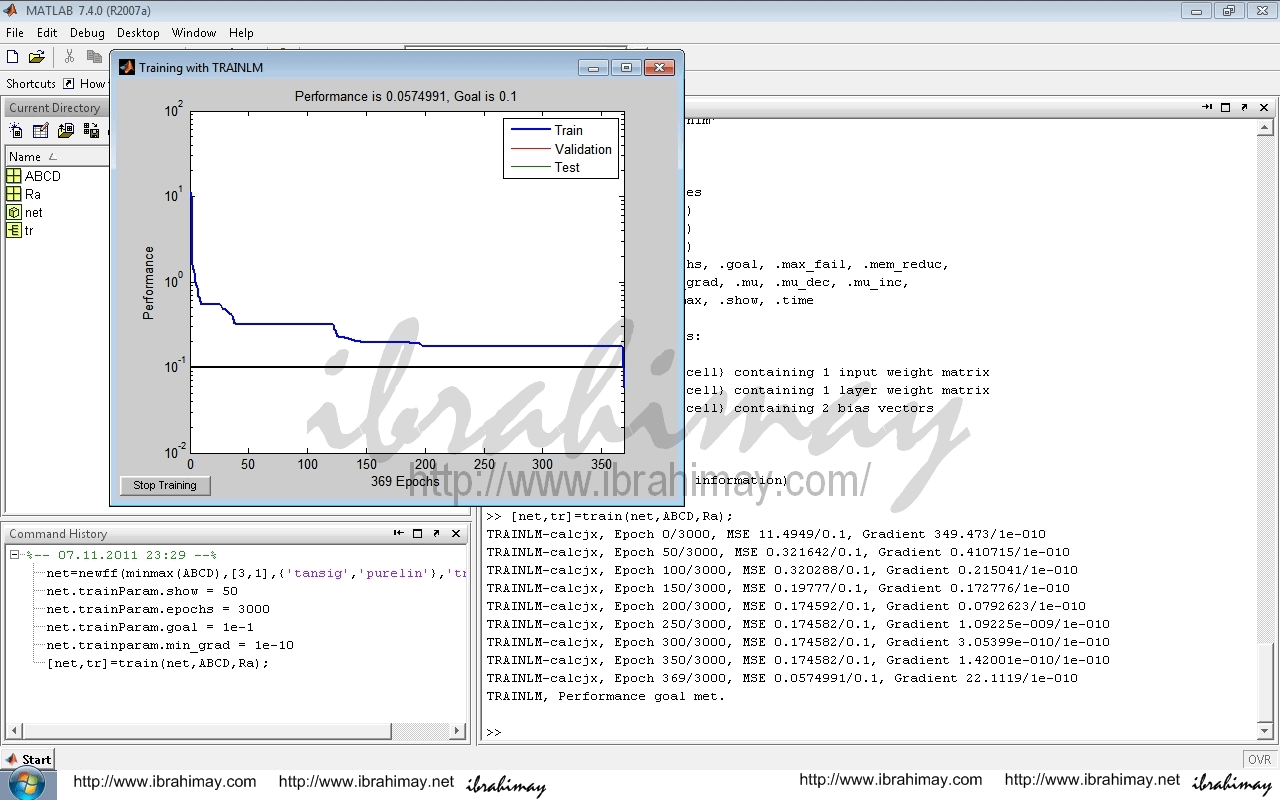
[net,tr]=train(net,ABCD,Ra);
369 döngü sonunda hedeflediğim 1e-1’lik MSE değerini yakaladım. Eğer başarılı olamaz isek [net,tr]=train(net,ABCD,Ra); ile eğitimi tekrarlayabiliriz. Ama öncelikle net = init(net); ile eğitimi sıfırlamamız iyi olur. Şimdi çıktımızı alalım ve gerçek değerlerle beraber görelim.
>>sonuc=sim(net,ABCD)
>>Ra
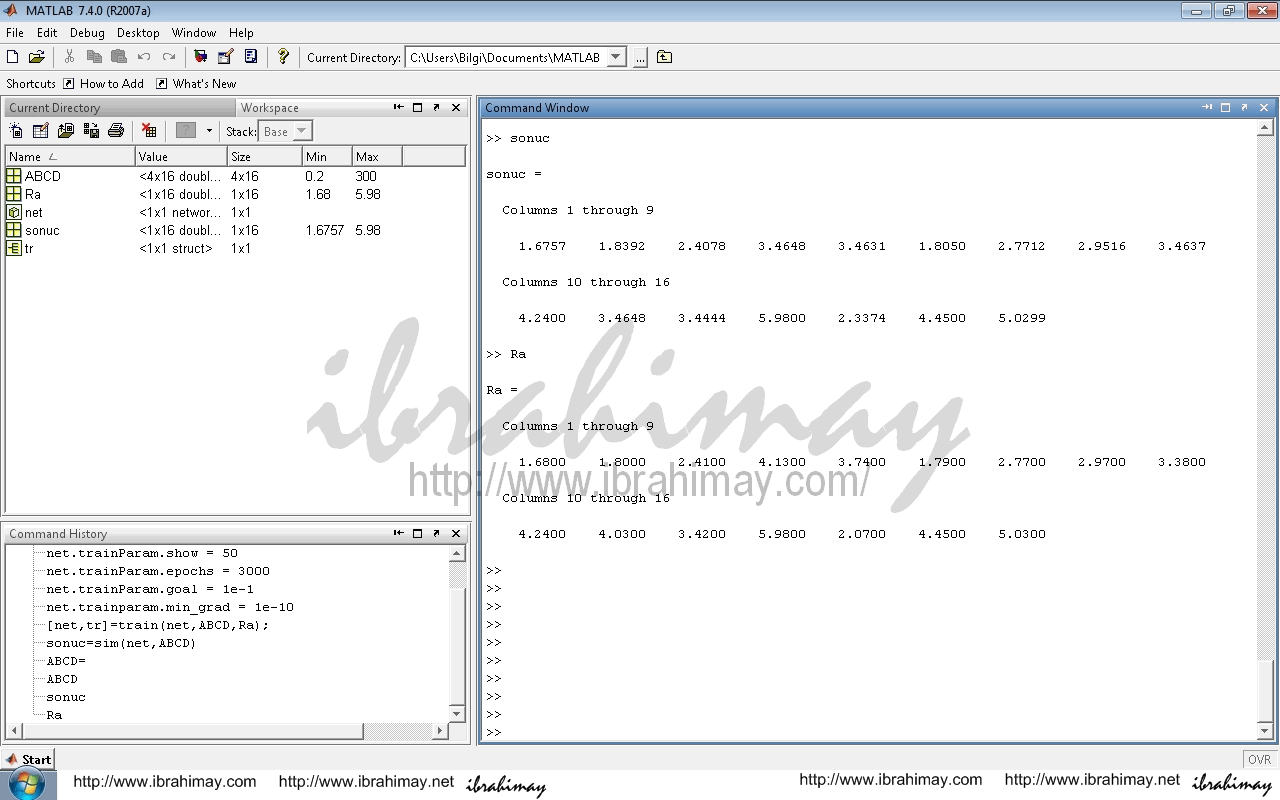
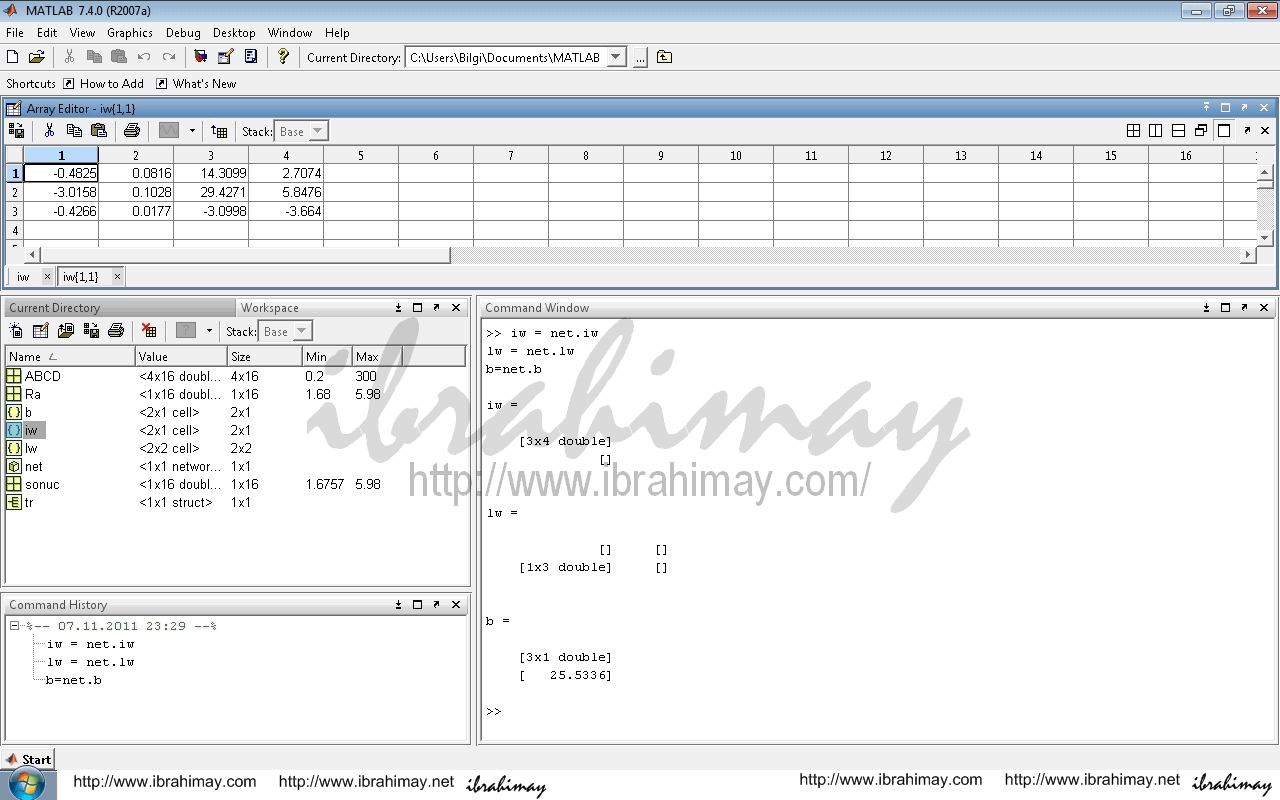
Şimdide ağırlıklarımızı ve sabitlerimizi alarak ağın denklemini çıkaralım. Burada işleyişi anlatmak için denklemleştiriyorum. Yoksa uygulamalarda o kadar çok nöron ve katman kullanırız ki denkleme dökmek zulümdür. Hatta katsayıları bile vermeyiz. Kim yazacak o kadar kalabalığı. Ama yazmakta fayda var. Katsayılar için şu komutları kullanabiliriz;
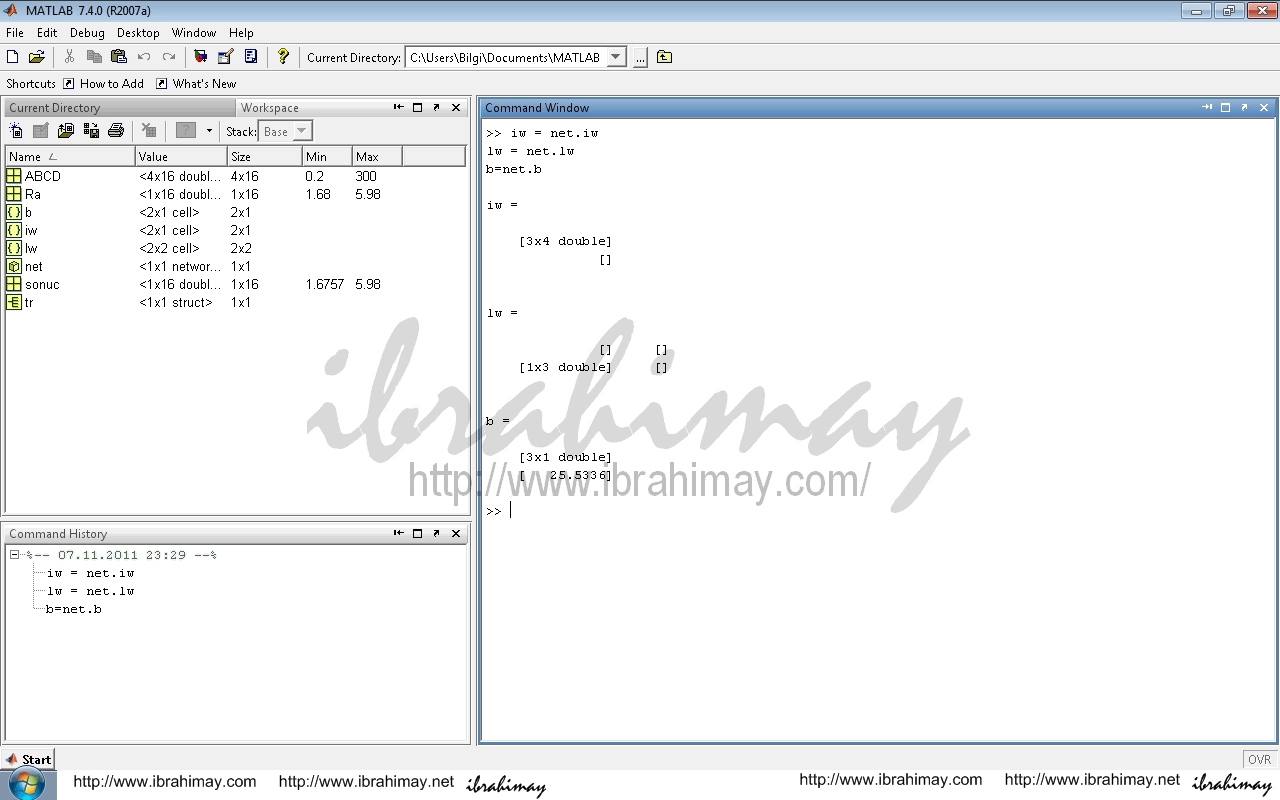
iw = net.iw
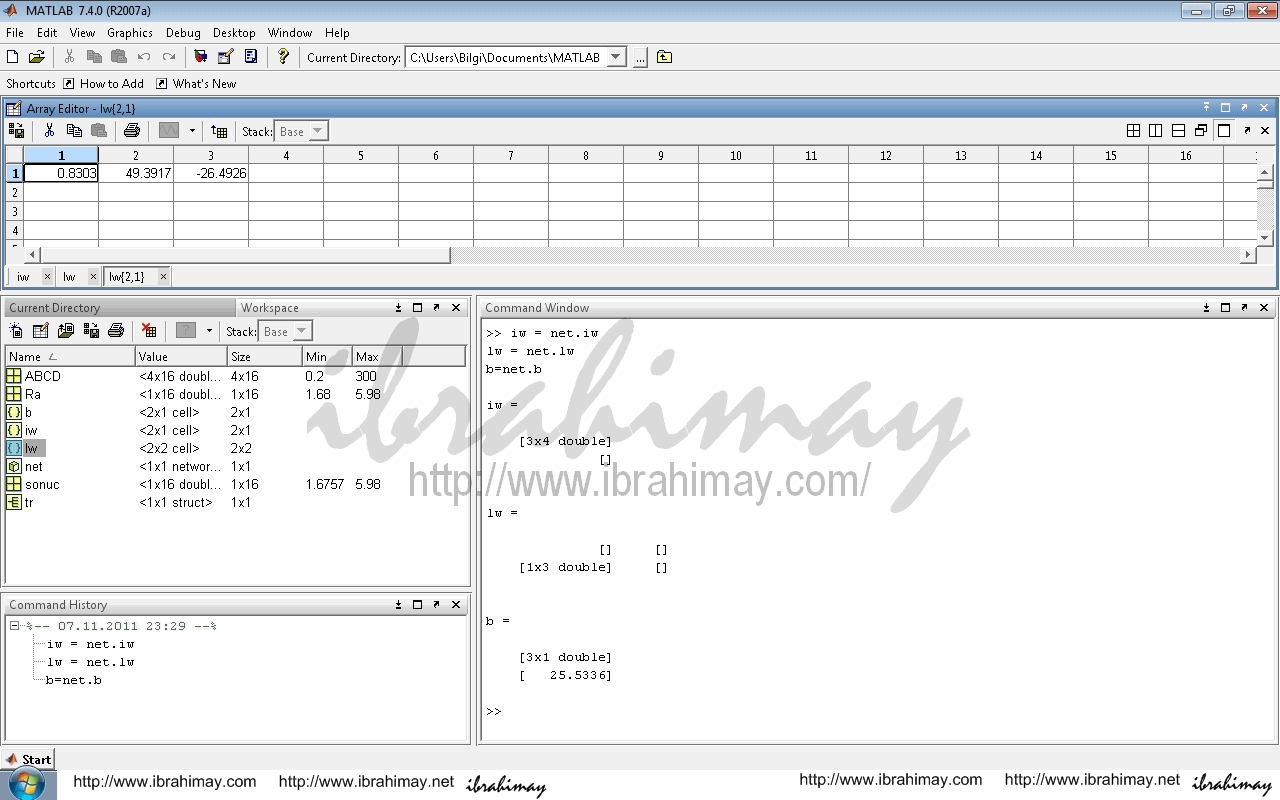
lw = net.lw
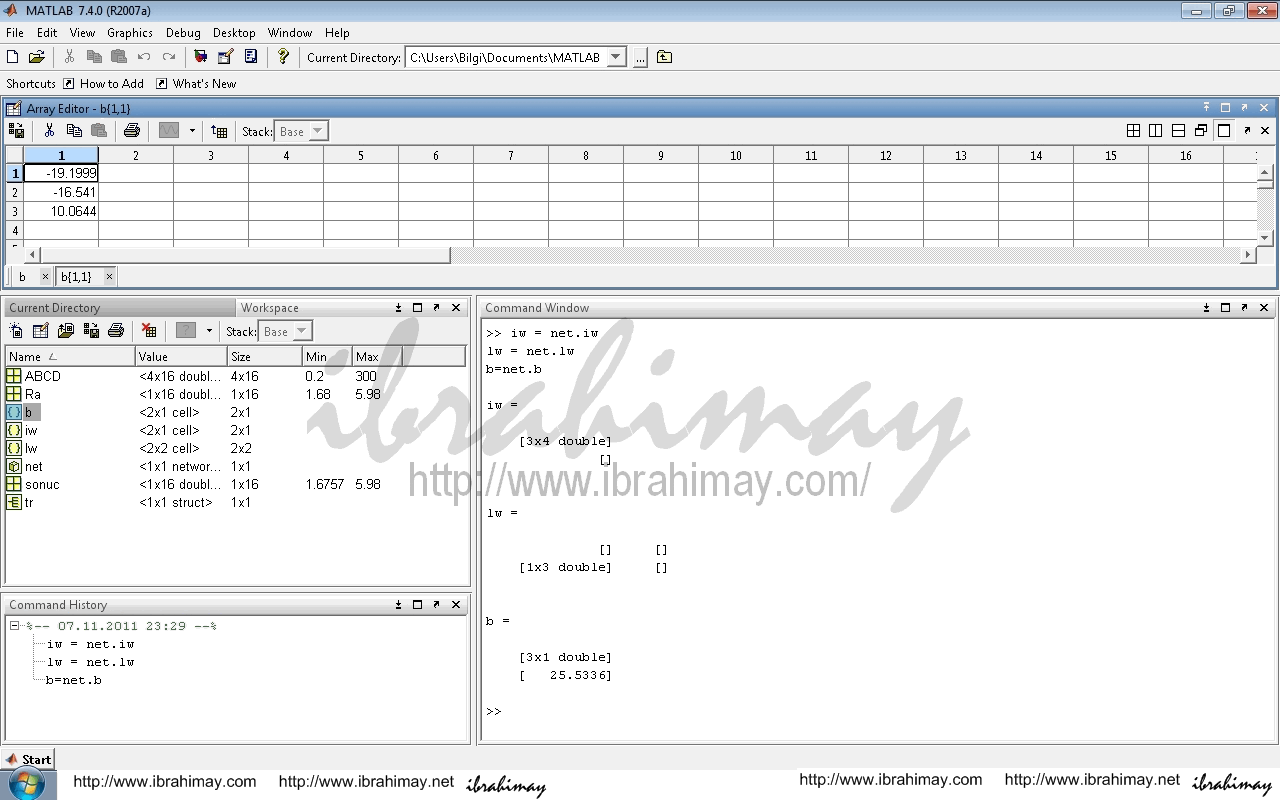
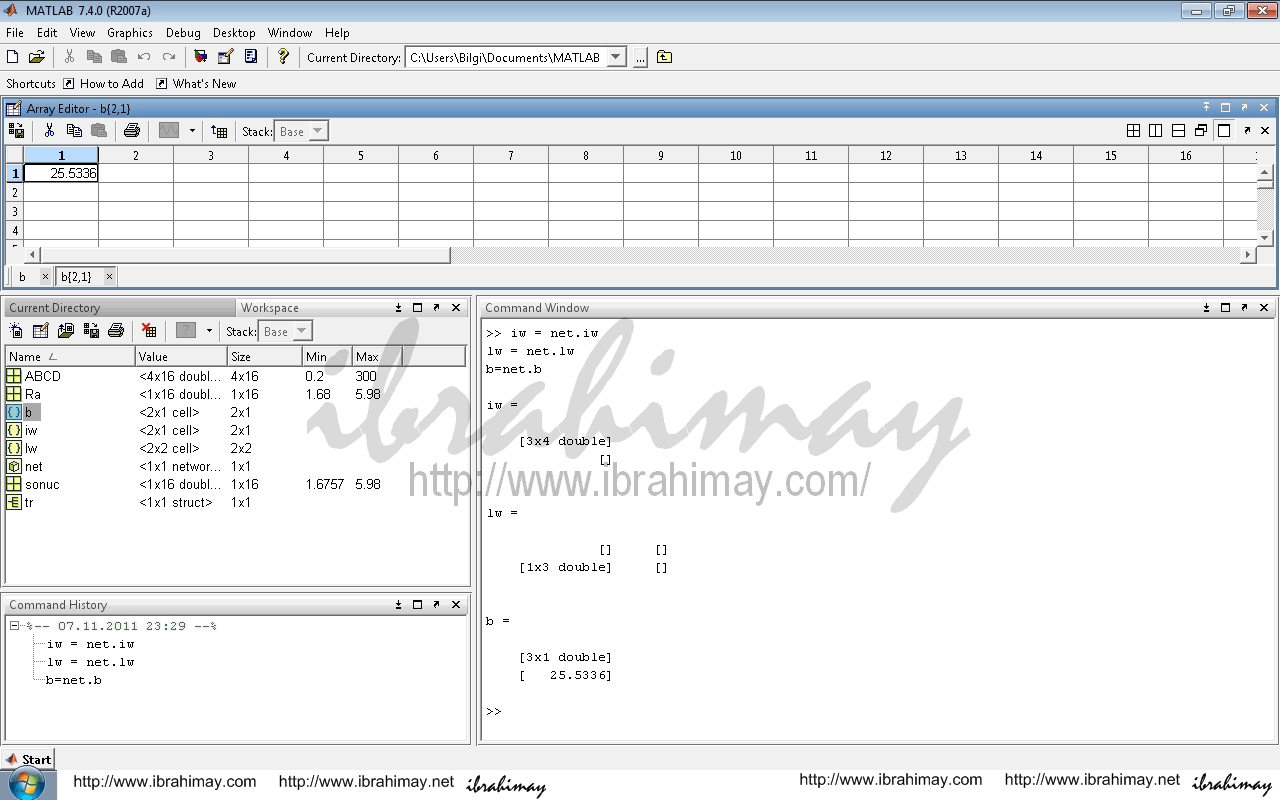
b=net.b

Verileri tablodan detaylı okumaya ihtiyaç duymaz iseniz aşağıdaki komutlar ile de ekrana bastırabilirsiniz:
bias1 = net.b{1}
bias2 = net.b{2}
weightsiw = net.iw{1}
weightslw = net.lw{2}
Katsayılarımız şöyle
| iw11-12-13 | b1 | |||
| -0.4825 | 0.0816 | 14.3099 | 2.7074 | -19.1999 |
| -3.0158 | 0.1028 | 29.4271 | 5.8476 | -16.541 |
| -0.4266 | 0.0177 | -3.0998 | -3.664 | 10.0644 |
| lw21 | b2 | |||
| 0.8303 | 49.3917 | -26.4926 | 25.5336 | |
Ağın denklemini daha anlaşılabilir olması için parçalı gösteriyorum:
1.nörona ==> -0.4825*A + 0.0816*B + 14.3099*C + 2.7074*D + -19.1999 = N1
2.nörona ==> -3.0158*A + 0.1028*B + 29.4271*C + 5.8476*D + -16.541 = N2
3.nörona ==> -0.4266*A + 0.0177*B + -3.0998*C + -3.664*D + 10.0644 = N3
Şimdide tansig fonksiyonundan geçiriyoruz:
Sonuç ==> {[2/(1+exp(-2*N1))-1]*0.8303} + {[2/(1+exp(-2*N2))-1]*49.3917} + {[2/(1+exp(-2*N3))-1]*-26.4926} + 25.5336
Not: exp(a)’nın ekselde çözümü üs(a)’dır. Veya matematikte e^a demektir. Misal exp(5)=üs(5)=e^5=148.4132
1. verinin çıktısını bulalım (17, 120, 0.2, 2)
1.nörona ==> -0.4825*17 + 0.0816*120 + 14.3099*0.2 + 2.7074*2 + -19.1999 = N1 = -9,33362
2.nörona ==> -3.0158*17 + 0.1028*120 + 29.4271*0.2 + 5.8476*2 + -16.541 = N2 = -37,89298
3.nörona ==> -0.4266*17 + 0.0177*120 + -3.0998*0.2 + -3.664*2 + 10.0644 = N3 = -3,01176
Sonuç ==> {[2/(1+exp(-2*-9,33362))-1]*0.8303} + {[2/(1+exp(-2*-37,89298))-1]*49.3917} + {[2/(1+exp(-2*-3,01176))-1]*-26.4926} + 25.5336
Sonuç ==> -0.8303 – 49.3917 + 26.3646 + 25.5336 = 1.6762
YSA çıktımız 1.6757’dir. Biz 1.6762 bulduk çünkü katsayılarda virgülden sonra 4 hane kullandık. Dolayısıyla bu kadar hatalı hesaplamamız çok doğal.
Toolbox İle YSA
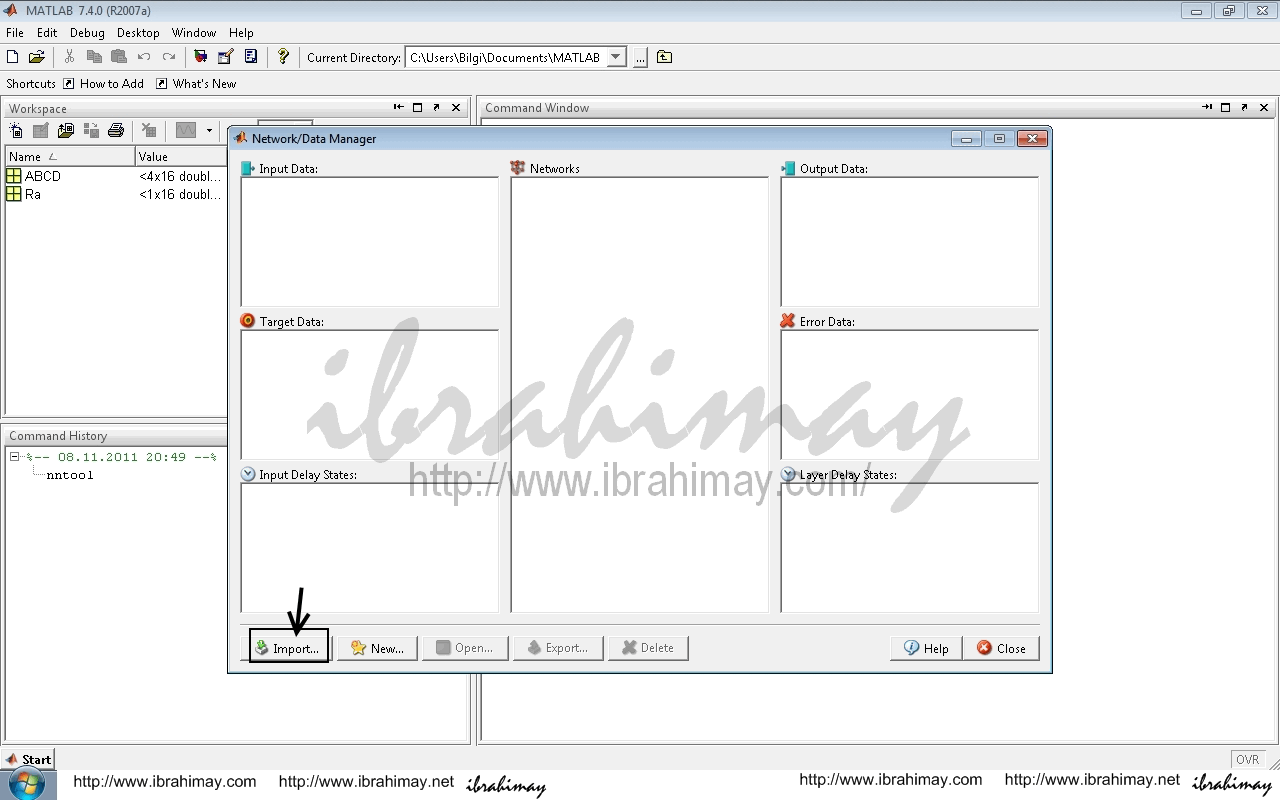
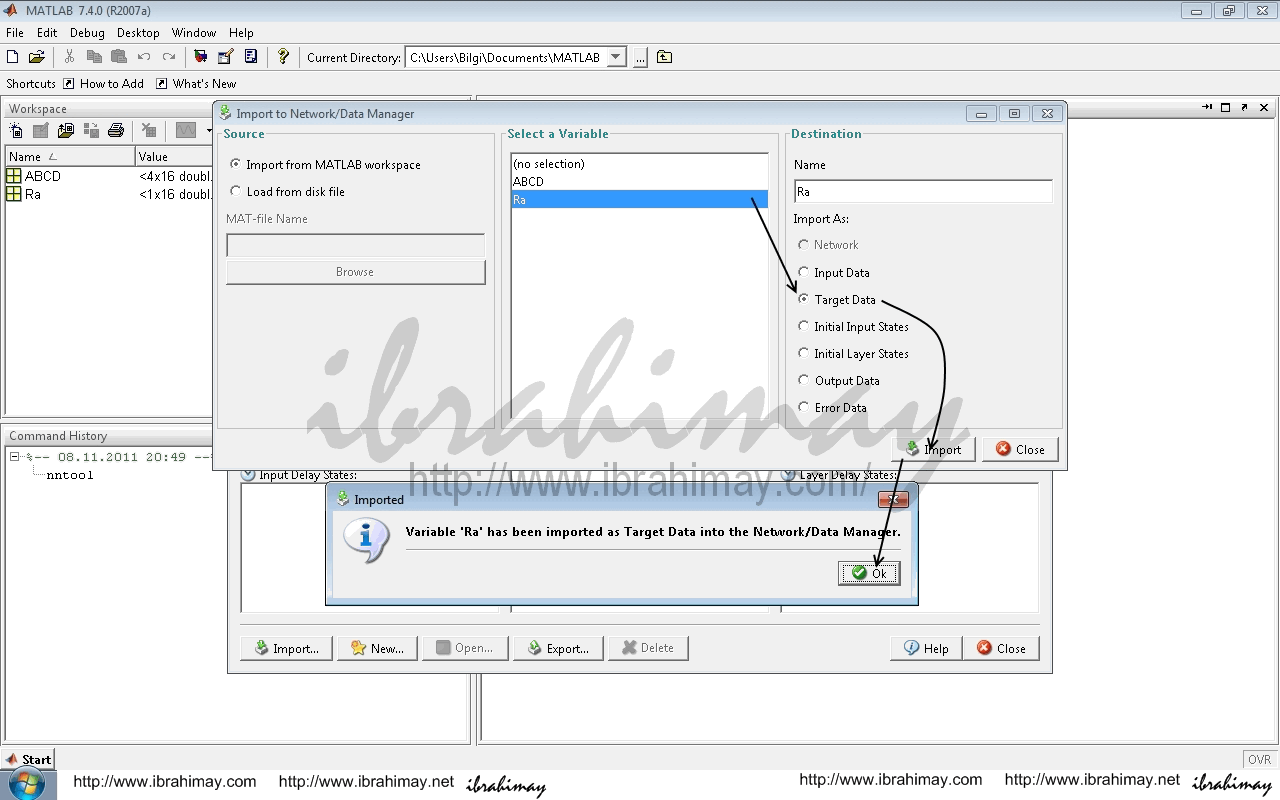
Yukarıdaki eğitimi toolbox ile yapalım. nntool komutunu yazdığımızda karşımıza çıkan network data penceresinde verilerimizi gireceğiz.
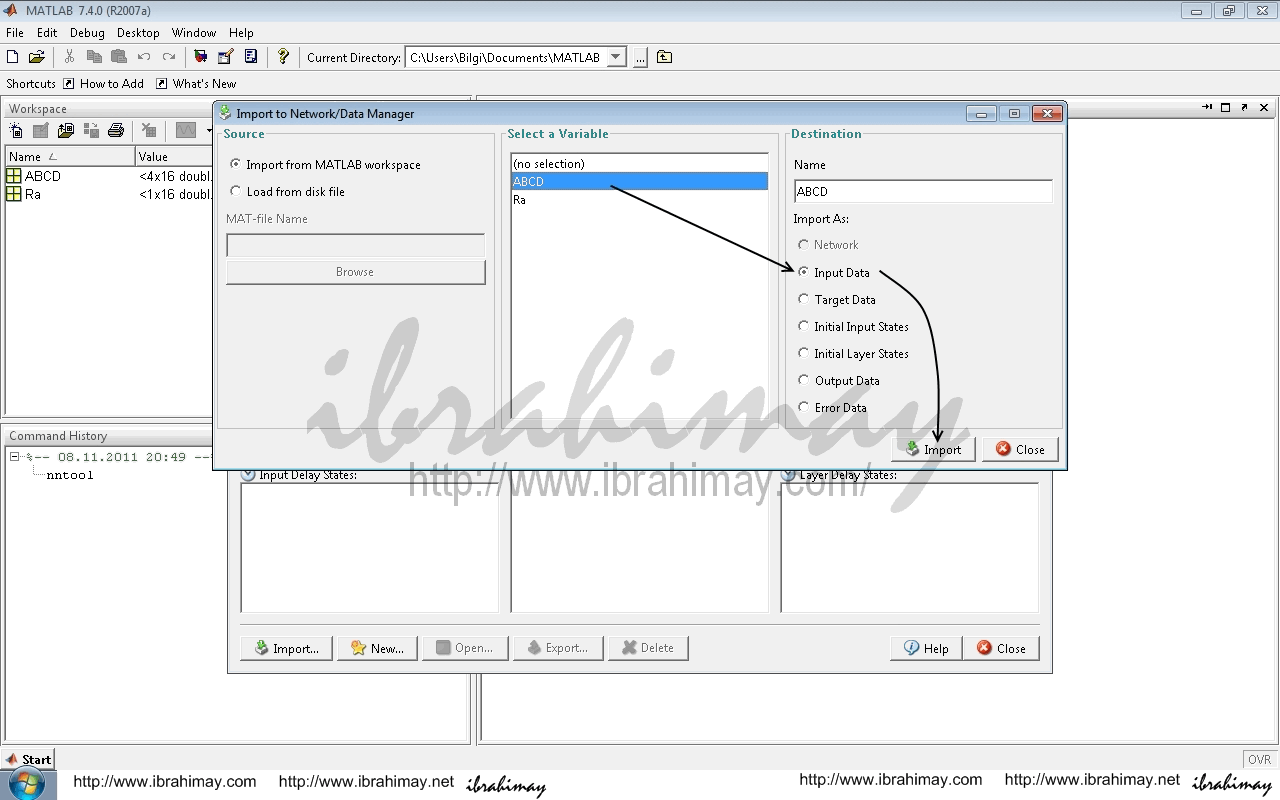
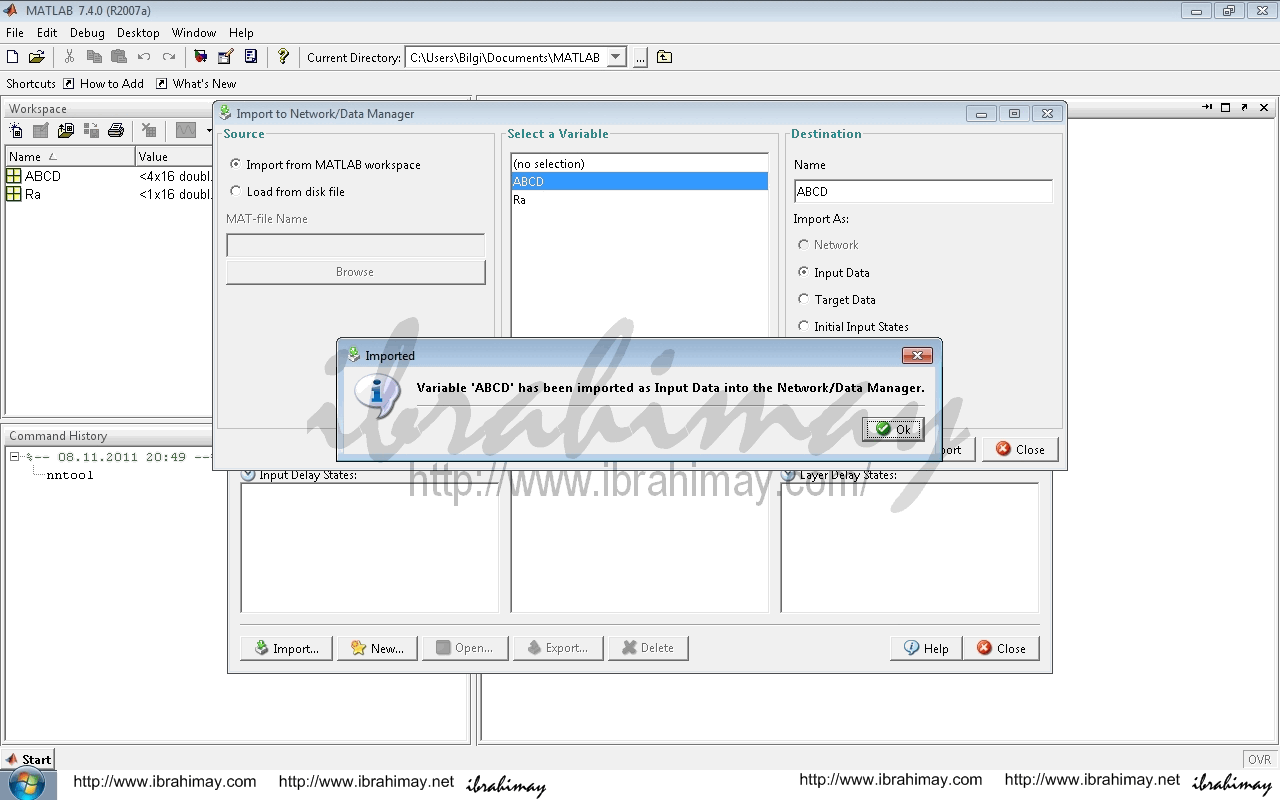
Bunun için İmport ile açılan pencerede ABCD seçilir. Değerlerimiz giriş verileri olduğu için sağda input data işaretlenerek import edilir.
Aynı işlem çıkış değerleri olan Ra için target data seçilerek gerçekleştirilir. Close ile bu pencereden çıkılır.
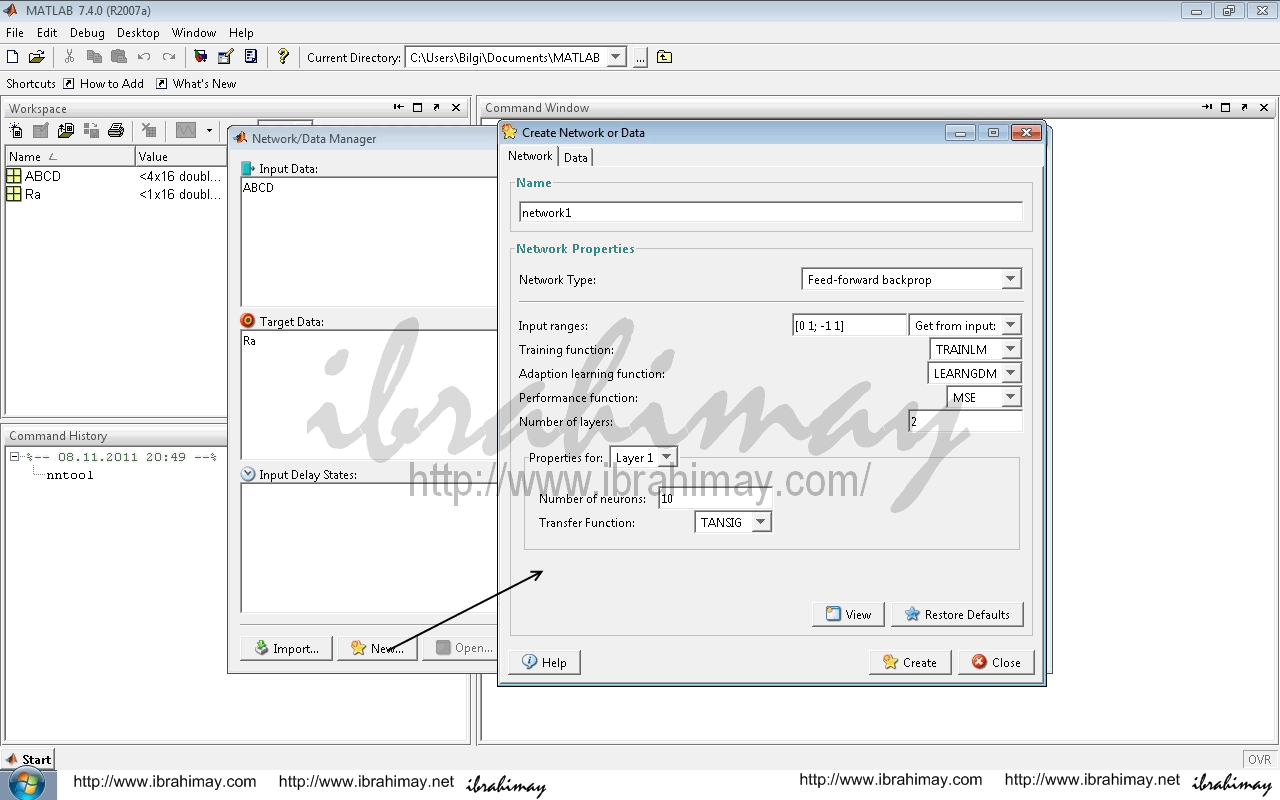
New komutu ile ağ tanımları yapılır.
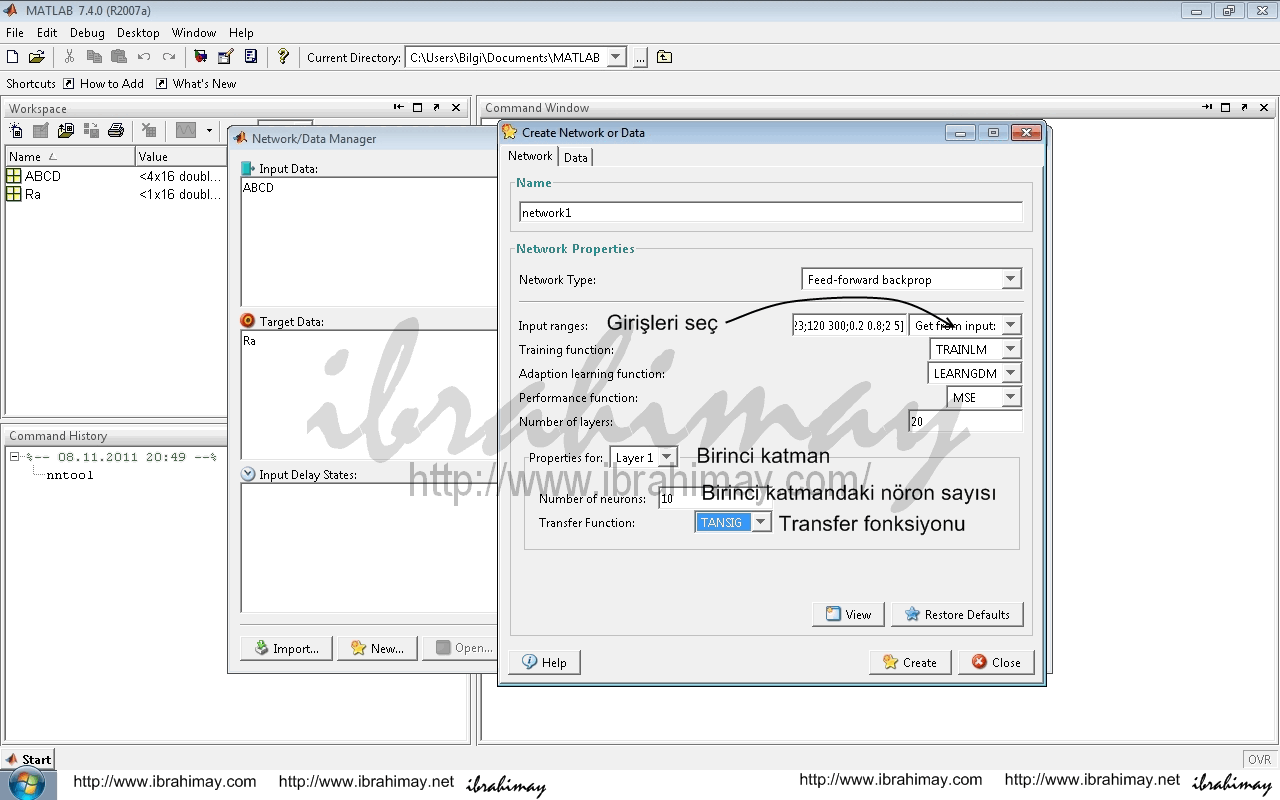
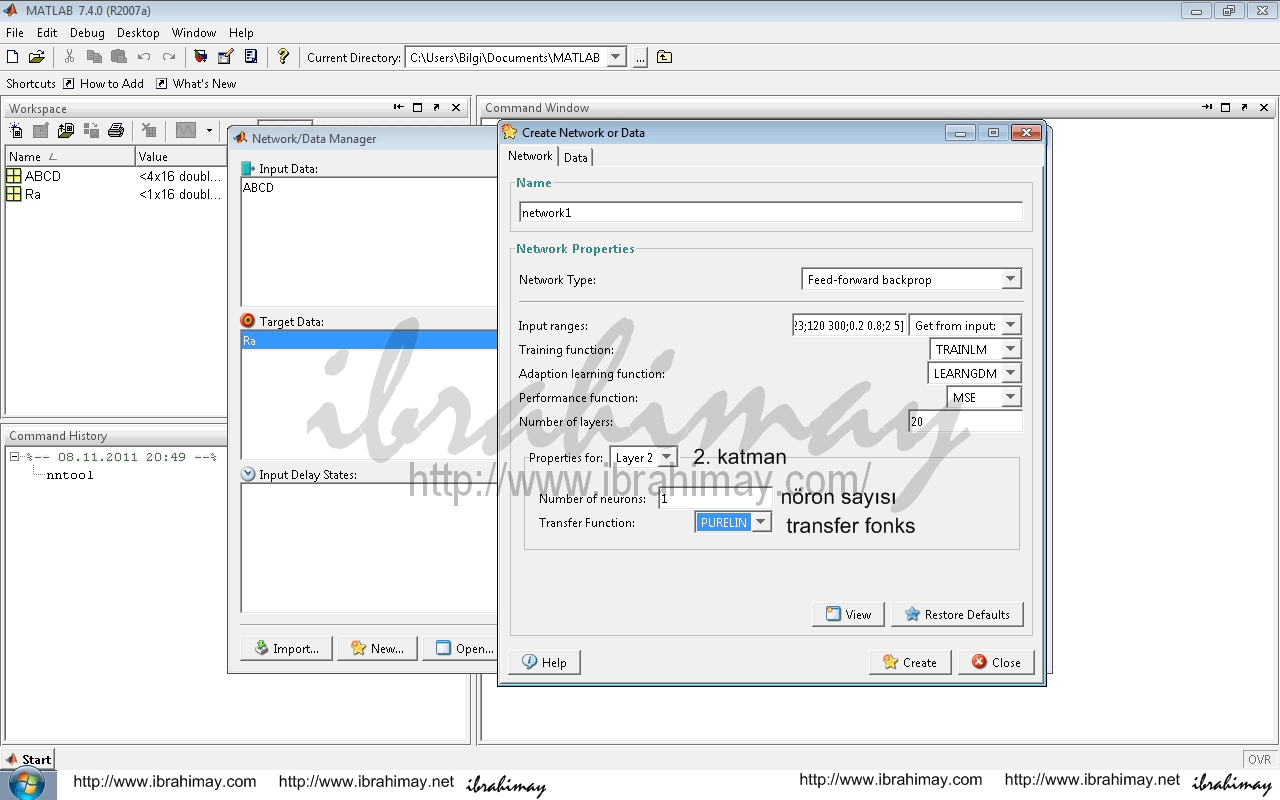
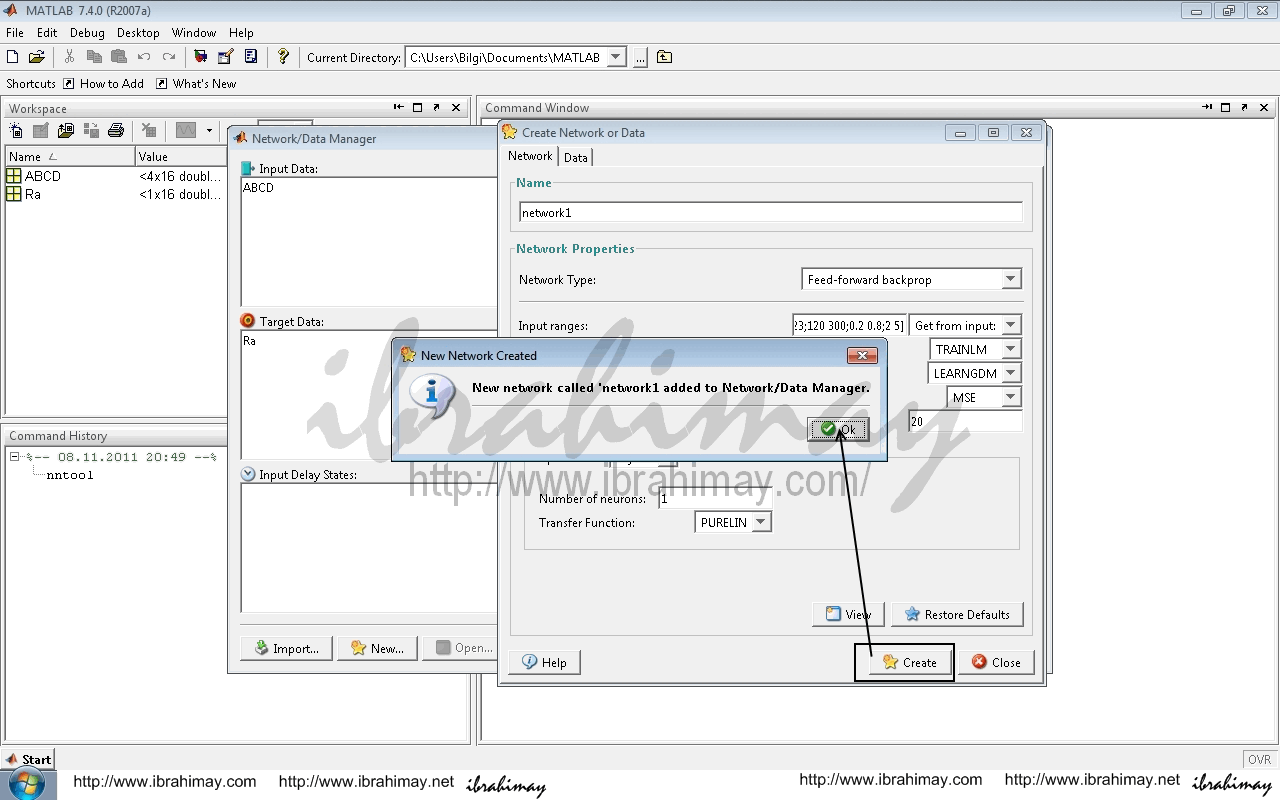
Create Network Or Data penceresinde İnput Ranges kısmı giriş verileri olarak seçilir (örneğimizde ABCD). Eğitim algoritması, nöron sayısı gibi çeşitli tanımlar isteğe göre doldurulur veya seçilir. Create ile işlem bitirilip close ile çıkılır.
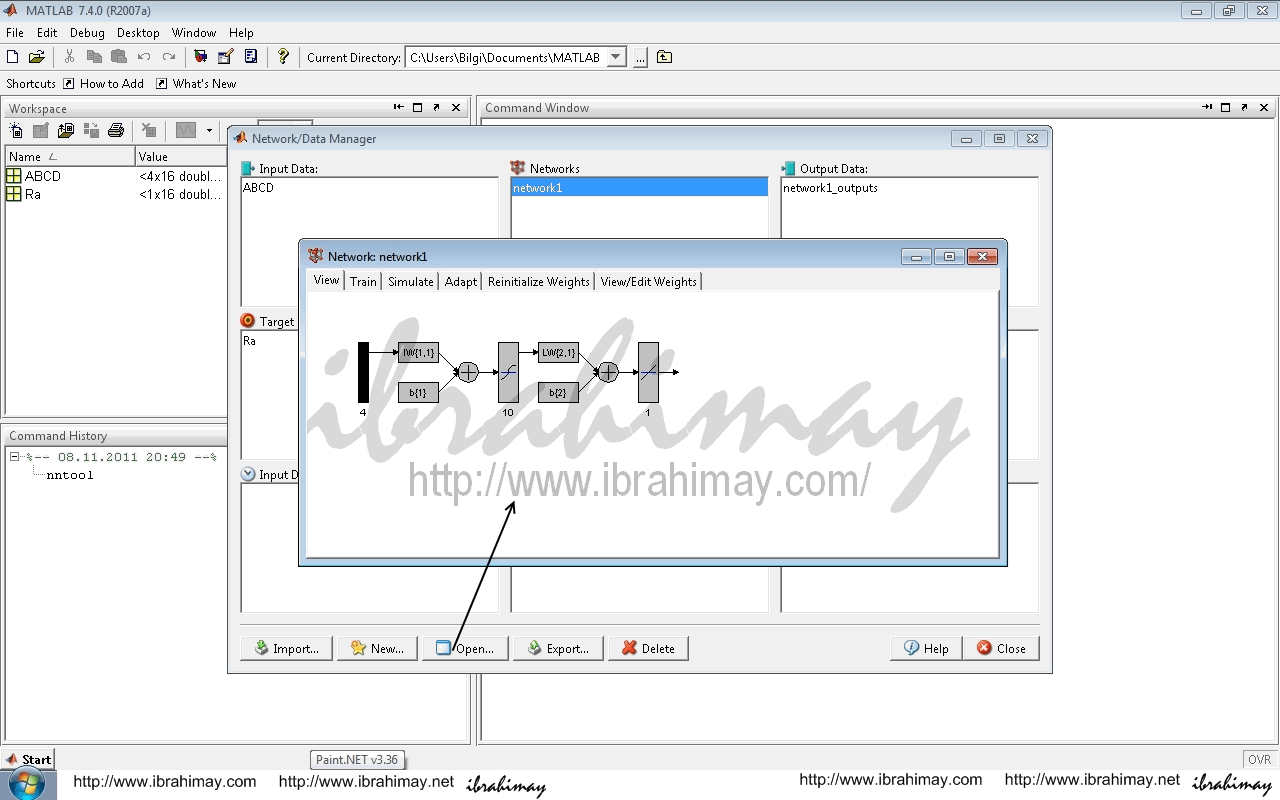
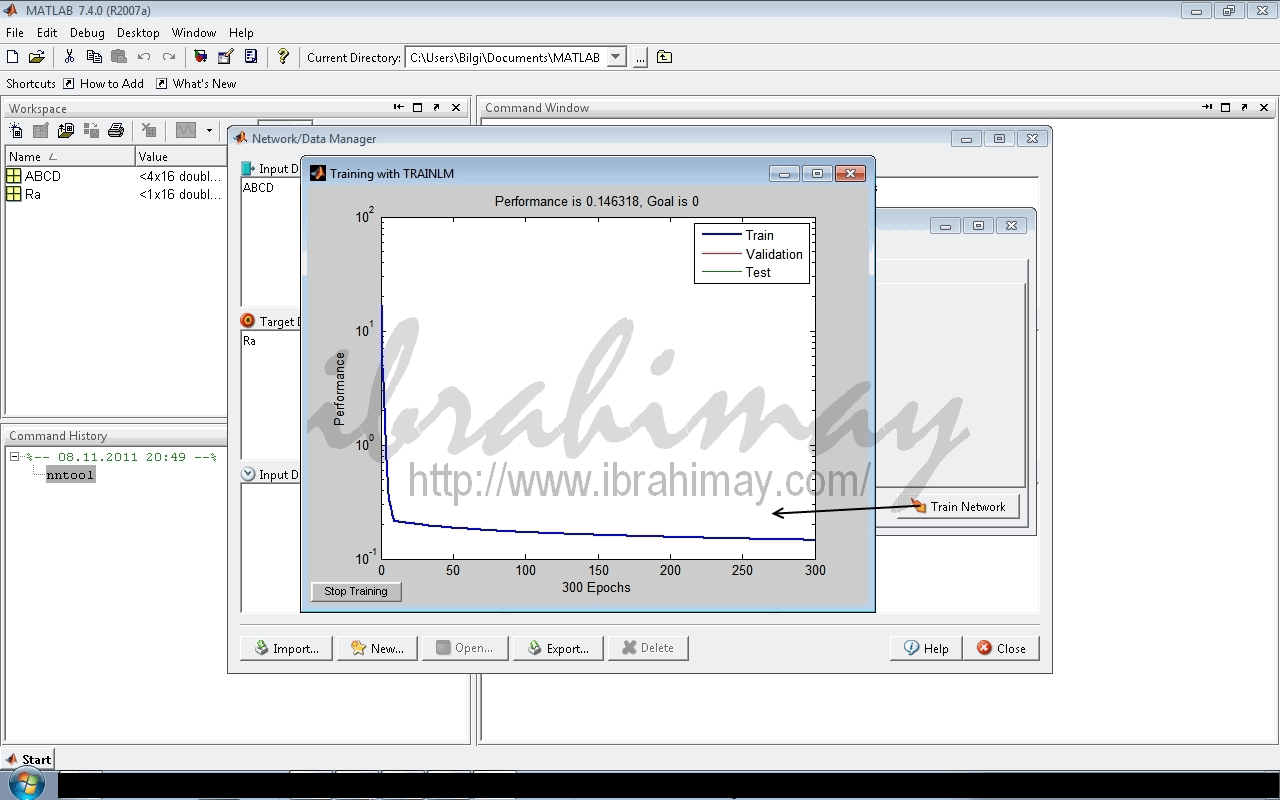
İşlenecek olan network1 ağımız çift tıklanarak veya open ile açılır.
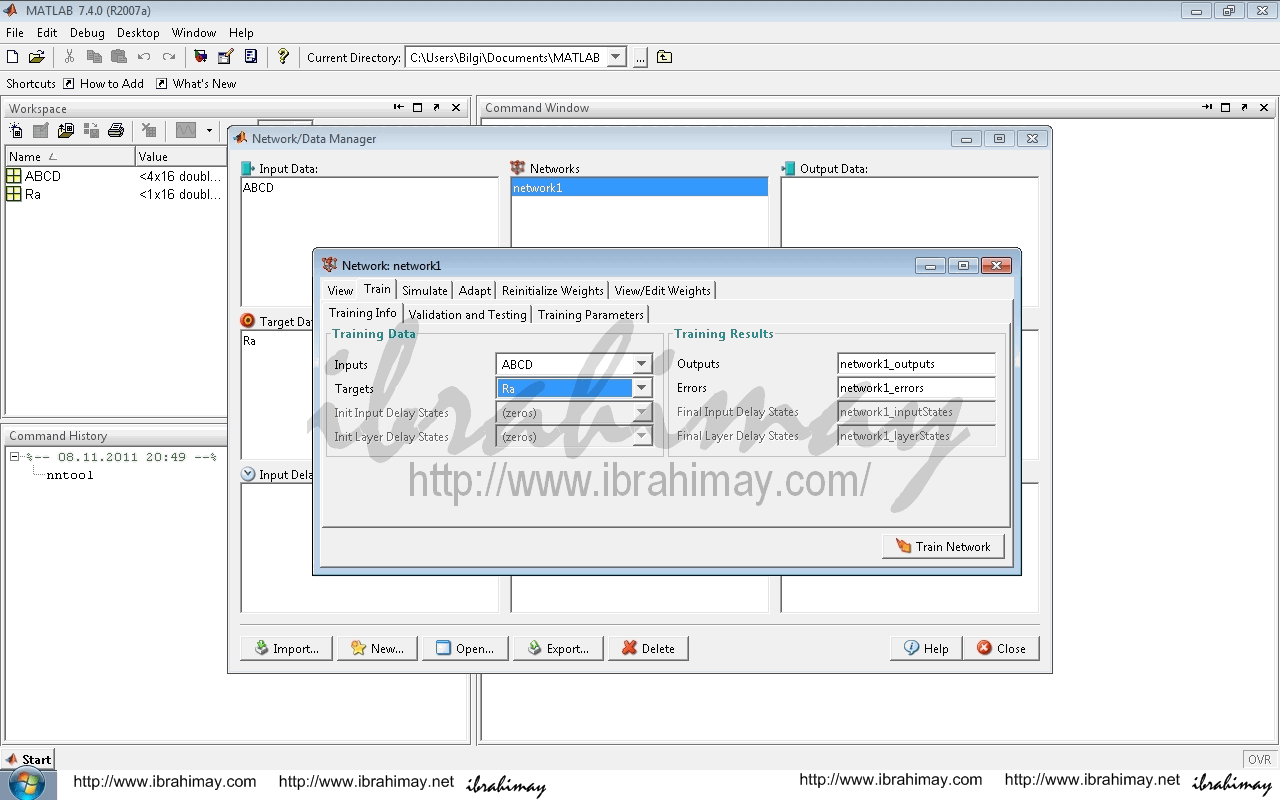
Train–>Training İnfo altında İnput için girişler, Target için çıkış (çıkışlar) tanıtılır. Train Network ile ağ eğitilir.
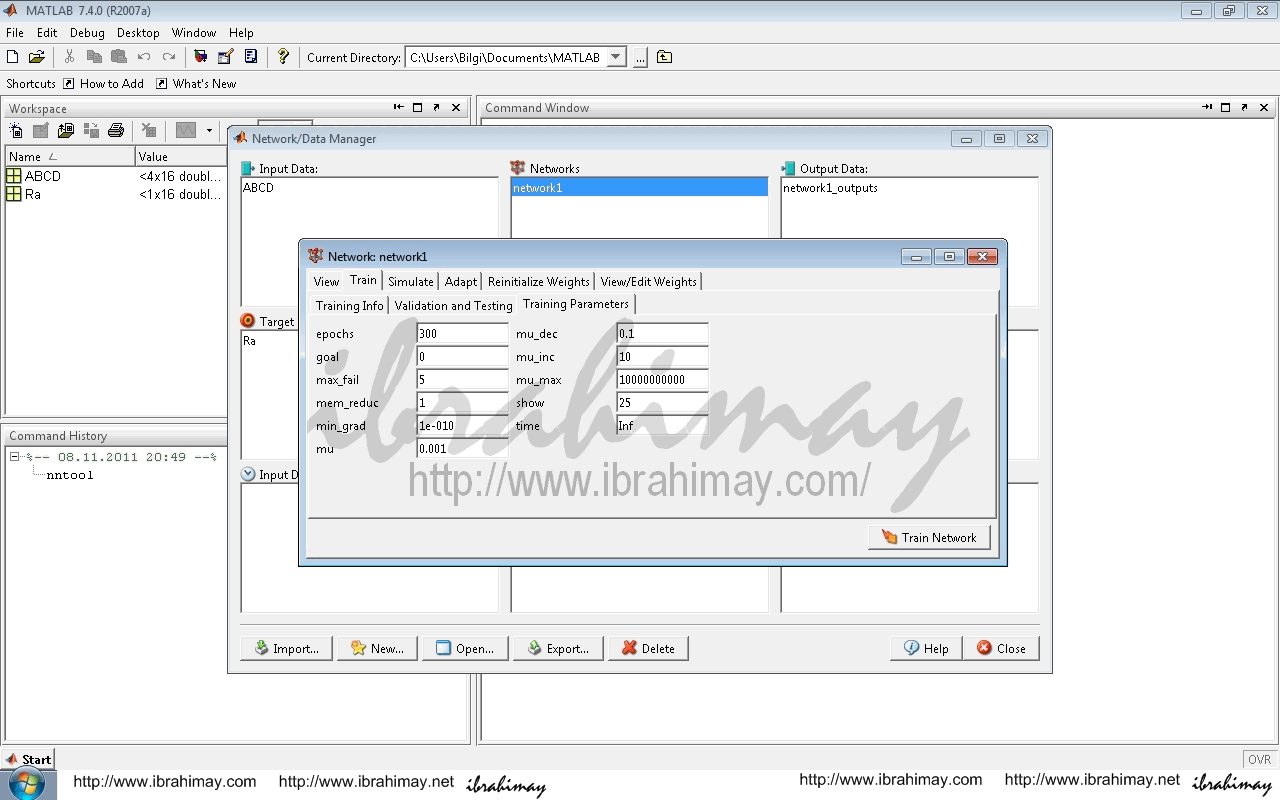
Eğitme işlemini Training parameter değerlerini değiştirerekte yapabilirsiniz.
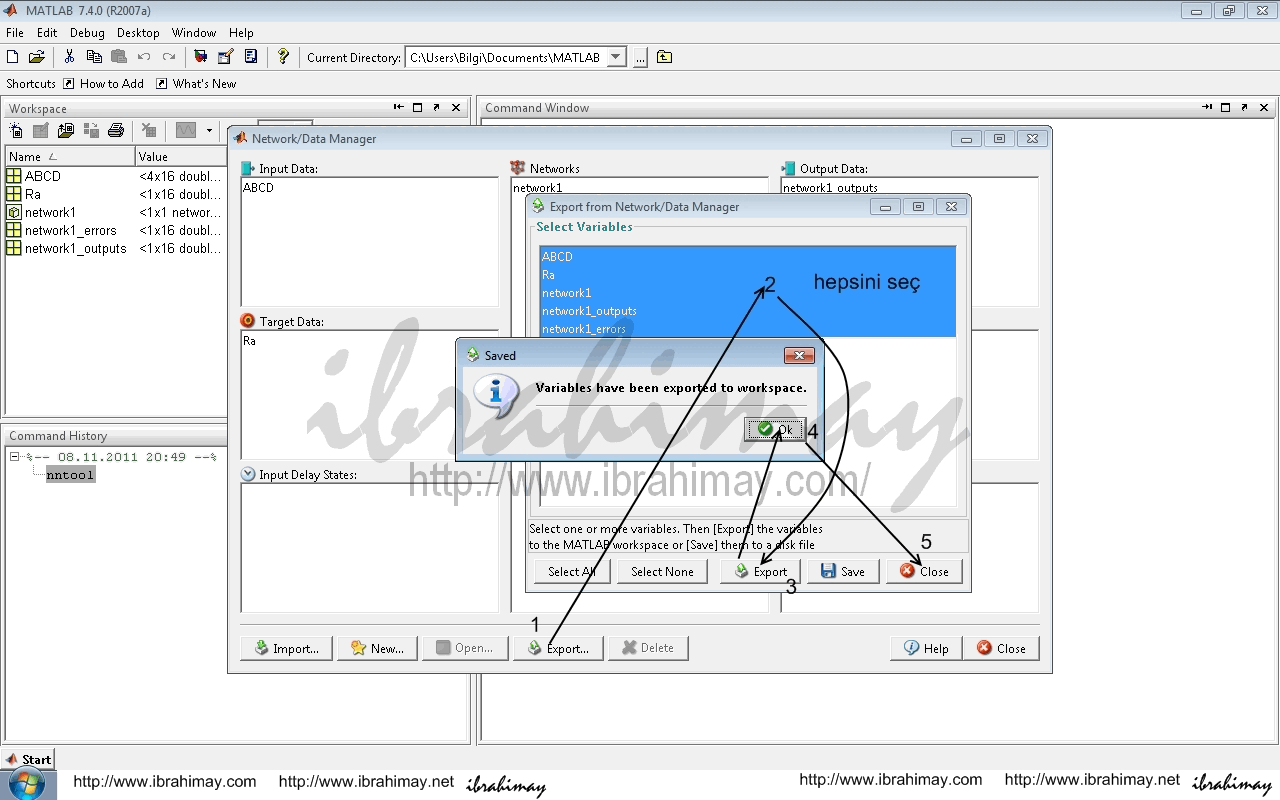
İşimiz bittiğinde export komutu ile verileri ve tabloları alabiliriz.
Şimdilik bu kadar. İyi dersler ve başarılar dilerim.







1 Response
[…] denklem için bura faydalı […]